Applications like protein interaction, cybersecurity, traffic forecasting, and molecular engineering often demand global insights that go beyond traditional graph-based representations. To capture such complexity, these domains benefit from models built on richer topological structures such as simplicial complexes, cell complexes, and hypergraphs.
Table of Contents
🎯 Why this matters
Purpose: Viewing graphs solely through a geometric lens often fails to capture non-local relationships and higher-order dependencies inherent in complex data. In many real-world applications—ranging from physical systems and social influence to traffic forecasting, protein interactions, and molecular design—data naturally exhibits rich topological structures such as edges, triangles, tetrahedra, and cliques.
Audience: This content is tailored for data scientists and researchers working on Geometric Deep Learning and Graph Neural Networks, who are looking to expand their understanding of topology-driven modeling.
Value: You’ll explore the core principles of Topological Data Analysis (TDA), learn about topological domains including simplicial complexes, cell complexes, combinatorial complexes, and hypergraphs, and follow a clear roadmap toward Topological Neural Networks.
🎨 Modeling & Design Principles
Overview
This article marks the first installment in our series on Topological Deep Learning using the TopoX and NetworkX libraries. It introduces the foundational concepts of Topological Deep Learning, setting the stage for upcoming hands-on articles that explore computations on structures such as simplicial complexes, cellular complexes, and topological networks.
📌 While this newsletter typically emphasizes hands-on applications across various areas of Geometric Deep Learning, this article is devoted to the underlying concepts and theory of Topological Data Analysis and Topological Deep Learning, and does not include source code.
Some Clarification
A simple way to define Topological Deep Learning (TDL) is by contrasting it with related fields in AI, such as Topological Data Analysis and the broader domain of Geometric Deep Learning.
📌 Throughout this newsletter, I use the term “node”, which is commonly used to describe a vertex in a graph, although in academic literature you may also encounter the term “vertex” used interchangeably.
This section defines TDL in contrast with
Topological Data Analysis
Traditional machine learning pipeline
Geometric Deep Learning
Graph Neural Networks
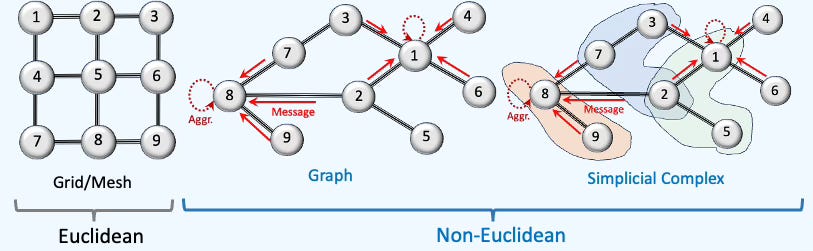
Fig. 1 Overview of Euclidean vs. Non-Euclidean Data Representation
Topological Data Analysis
The distinction between Topological Data Analysis (TDA) and Topological Deep learning (TDL) can be confusing as both stem from algebraic topology.
While TDA supports analysis of the shape of input data (e.g., outliers, clusters,..) [ref 1], TDL is used to build learning models (e.g., Graph, Node, Simplex classification) that exploits both the input data and the output of TDA as illustrated below:
Fig. 2 Generic TDA/TDL Data Pipeline
Objective:
TDA: Extract topological features from input data
TDL: Leverage topological features as prior to the deep learning model
Scope:
TDA: Features engineering and processing
TDL: Model design, training, validation and test
📌 TDA techniques can be applied independently from TDL for anomaly detection, shape clustering, discontinuity, voids identification.
ML Pipeline
One might ask how incorporating topological domains affects the workflow for training and evaluating machine learning models.
The preprocessing stage must be extended to include the construction of topological structures—such as simplicial or combinatorial complexes—which serve as enriched inputs for the modeling phase.
Topological deep learning models adopt core architectural principles from Graph Neural Networks (GNNs), such as message passing.
Model evaluation combines traditional machine learning metrics with topology-aware measures, including persistent homology and equivariance scores, to assess the model's ability to capture and preserve topological features.
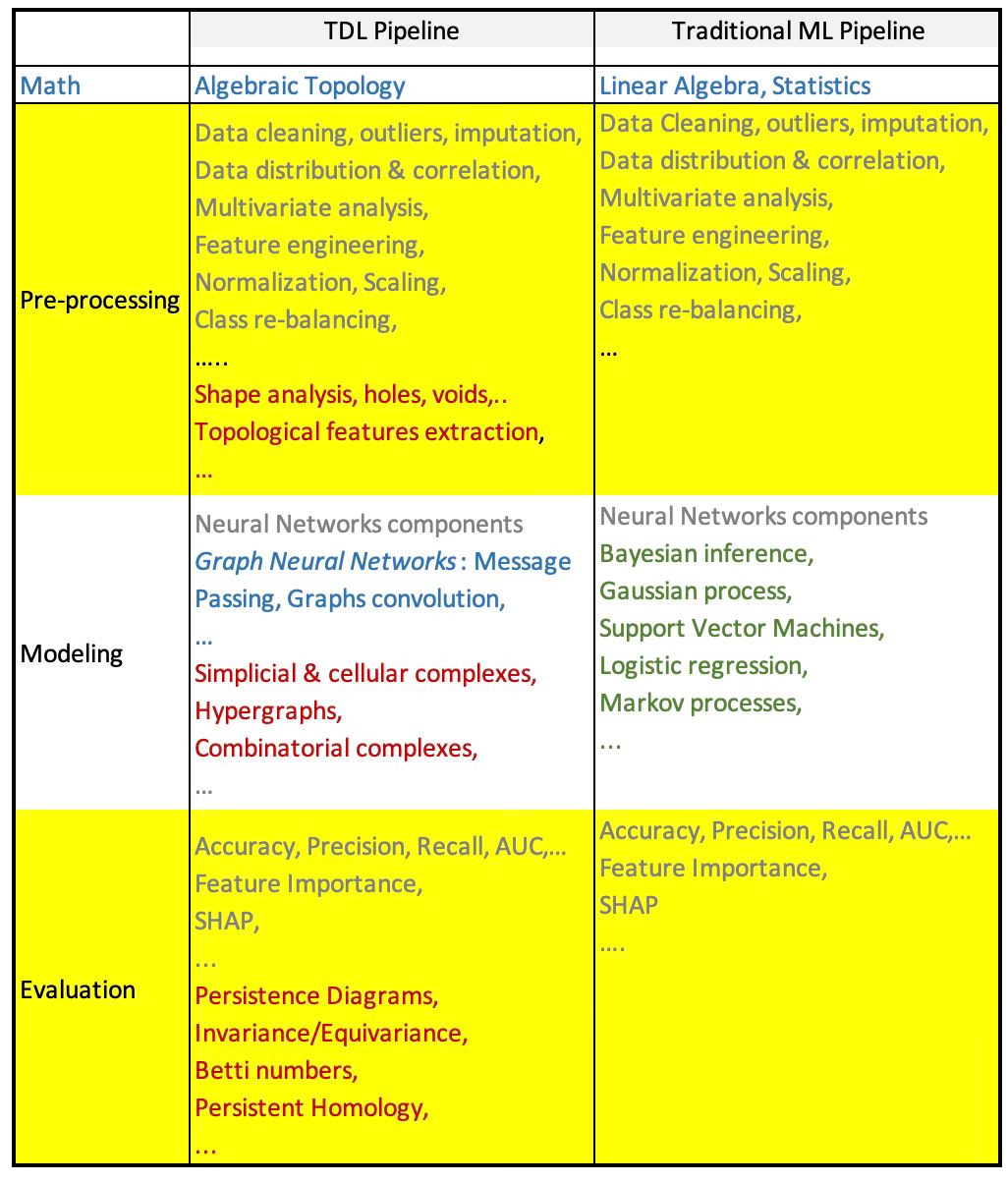
The following comparison tables illustrates the difference between traditional machine learning pipeline and TDL pipeline.
Table 1 Comparison TDL and traditional ML pipelines
Geometric Deep Learning
TDL is widely considered a subfield of Geometric Deep Learning (GDL).
Geometric Deep Learning refers to the study and design of neural networks that operate on non-Euclidean domains, such as Graphs, Manifolds, Lie groups, Simplicial and cellular complexes, Riemannian structures, It unifies methods that respect geometric priors, symmetry, and structure in data — including spatial locality, equivariance, and relational constraints [ref 2].
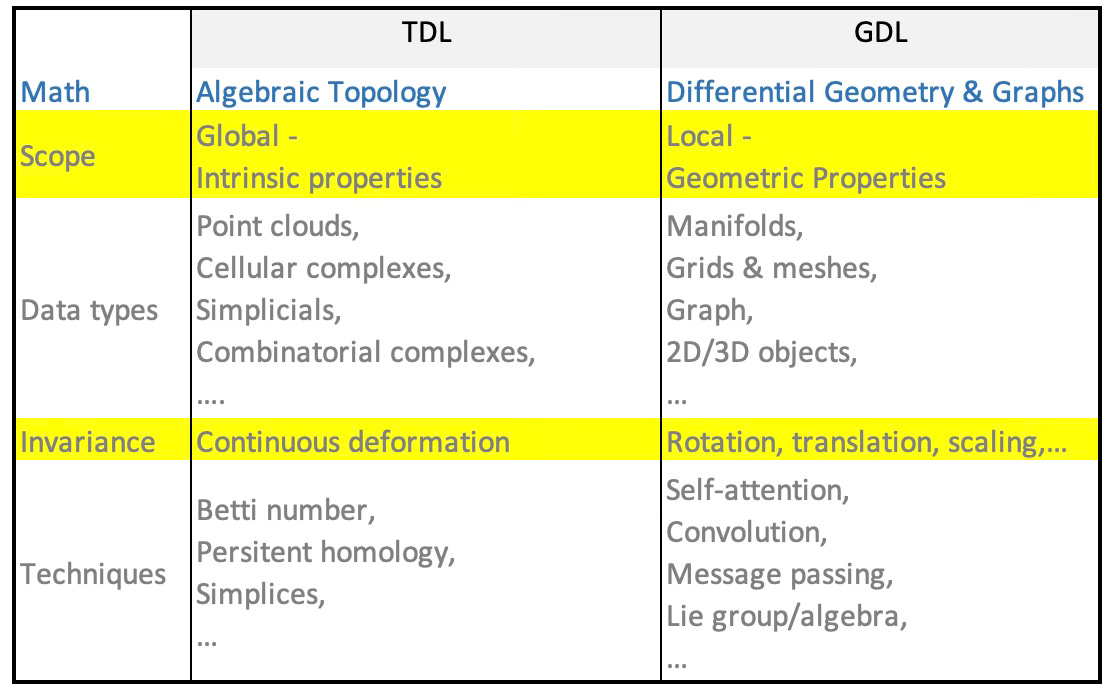
There are some subtle differences as detailed in the next table.
Table 2 Comparison TDL and GDL
Graph Neural Networks
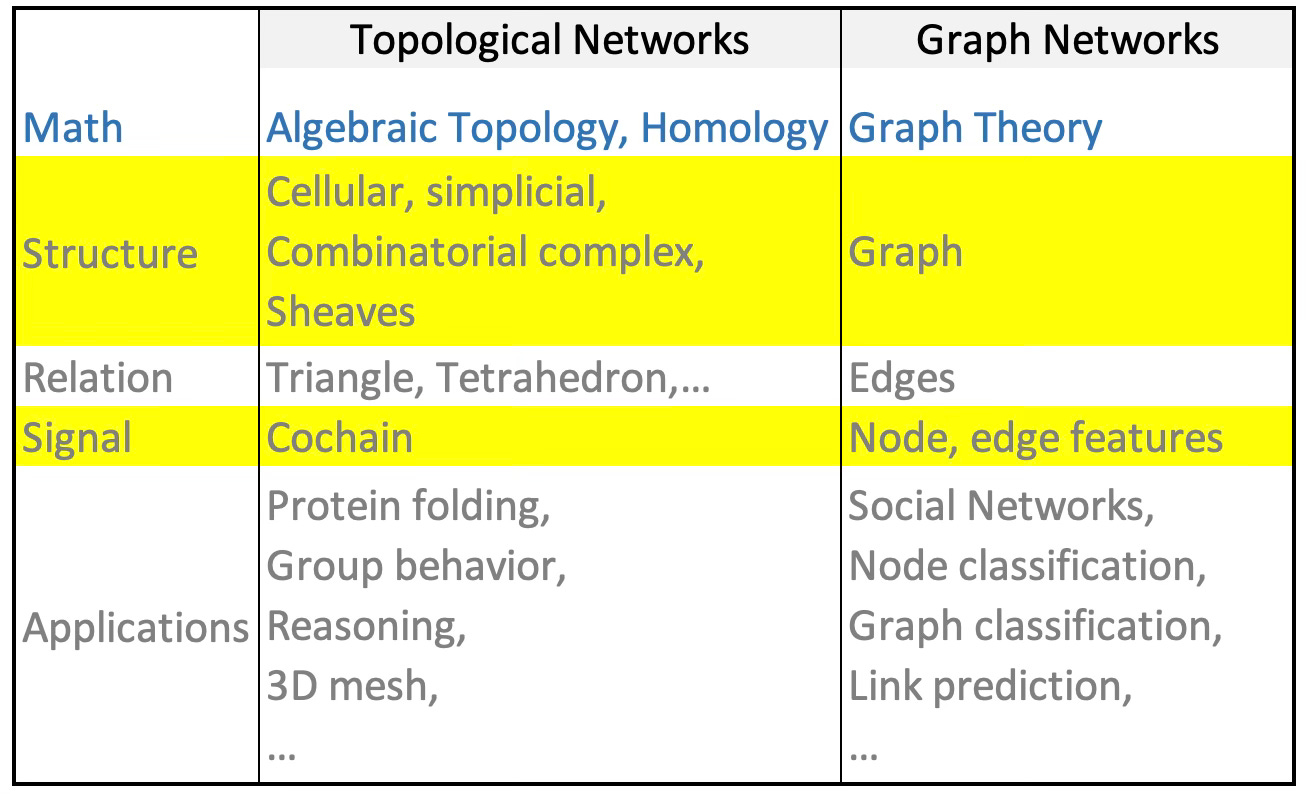
Graph Neural Networks are a 1-dimensional special case of Topological Deep Learning which enables deep learning on structures beyond graphs, with richer relational topologies [ref 3, 4 & 5]
Table 3 Comparison of Topological Networks and Graph Neural Networks
... and Some Definitions
The following alphabetic-ordered list of terms converts both data analysis (TDA) and modeling (TDL):
Betti number: A key topological invariant that count the number of certain types of topological features in a space. It provides a concise summary of the space's shape and structure, especially when dealing with high-dimensional or complex datasets (dimension 0: Connected components, dimension 1: holes, loops, dimension 2: 3D holes and voids,)
Category Theory: A branch of mathematics that deals with abstractions of mathematical structures and the relationships between them. It focuses on how entire structures relate and transform via morphism
Cellular (or CW, Cell) Complex: A topological space obtained as a disjoint union of topological disks (cells), with each of these cells being homeomorphic to the interior of a Euclidean ball. It is a general and flexible structure used to build topological spaces from basic building blocks called cells, which can be points, lines, disks, and higher-dimensional analogs.
Cochain (or k-Cochain): A signal, a function from a combinatorial complex of rank k to a real vector.
Cochain Map: A map between cochain spaces that use incidence matrix as transformation.
Cochain Space: The space of cochains.
Combinatorial Complex: A structured collections of simple building blocks (like vertices, edges, triangles, etc.) that models the shape of data in a way that is amenable to algebraic and computational analysis.
Filtration: A nested sequence of topological spaces (typically simplicial or cell complexes) built from data, where each space includes the previous one. Each of these topological spaces, represents the data’s topology at a certain scale or resolution.
Hausdorff Space: Topological space for which points are separable and can be included into their open sets that do not intersect.
Hypergraph: A generalization of a traditional graph where edges (called hyperedges) can connect any number of nodes, not just two. While edge of a graph models a binary relationship, a hypergraph models higher-order relationship among group of nodes
Homeomorphism. A morphism between two topological spaces is a bijective map for which a function and its inverse are continuous.
Homotopy: A fundamental idea in topology about continuously deforming one shape into another — like stretching, bending, or twisting — without tearing or gluing.
Incidence Matrix: An encoding of relationship between a k-dimensional and (k-1) -dimensional simplices (nodes, edges, triangle, tetrahedron,..) in a simplicial complex.
Persistent Homology: A method from TDA that captures the shape of data across multiple scales. It tracks topological features—such as connected components, loops, and voids—as they appear and disappear in a growing family of simplicial complexes.
Point Cloud: A collection of data points defined in a 3D space. These points represent the external surface of an object. A point cloud has spatial coordinate (x, y, z) and internal representation but does not contain any information about how points are connected (edges, faces,).
Pooling Operation: A pooling operation is a mechanism for reducing the complexity of topological input spaces (like graphs, simplicial complexes, or cell complexes) while preserving essential topological features.
Poset: A Partially Ordered Set which pear in causal structures, stratified space and singular manifolds. A poset is a set P equipped with a partial order <= satisfying (Reflexivity, Anti-symmetry, Transitivity).
Push-forward Operation: A way of transferring functions or signals defined on one topological domain to another, typically along a continuous or structure-preserving map. It's rooted in differential geometry and algebraic topology.
Relation: A subset of a set of vertices characterized by a cardinality (e.g., 2 for binary relation).
Sheave: A mathematical tool that helps track local data on a space and describes how it glues together consistently across overlapping regions. Sheaves generalize persistent homology by allowing richer types of data.
Simplex: A generalization of edge-bound shapes such as triangles, tetrahedron
Simplicial Complex: A generalization of graphs that model higher-order relationships among data elements—not just pairwise (edges), but also triplets, quadruplets, and beyond (0-simplex: node, 1-simplex: edge, 2-simplex: Triangle, 3-simplex: Tetrahedron, ).
Set-type Relation: A type of relation which existence is not implied by another relation within the graph (e.g., hypergraphs).
Topological Data: A set of feature vectors supported on relations in a topological space.
Topological Data Analysis (TDA): A framework that uses concepts from topology to study the shape and structure of data. It captures high-dimensional patterns, such as clusters, loops, and voids, by building simplicial complexes and computing topological invariants like Betti numbers. TDA is especially useful for revealing robust geometric features that persist across multiple scales in noisy or complex datasets.
Topological Deep Learning (TDL). An approach that incorporates ideas from topology, particularly algebraic topology, into deep learning. It focuses on the intrinsic, global properties of data that remain unchanged under continuous deformations, like stretching or bending, rather than the local structure of data.
Topological Group: A mathematical object that is simultaneously:
A group (an algebraic structure with an associative binary operation, identity, and inverses), and
A topological space (a set with a notion of continuity, open sets, etc.)
Topological Space: This is a set X with a collection of subsets T, known last open sets of X that satisfy:
Empty Set belongs to T
X belongs to T
Union of open sets is open
Intersection of open sets is open
Unspooling Operation: The counterpart to the pooling process. It reconstructs or expands a coarsened topological structure back to a finer-resolution space — typically to enable decoding, up-sampling, or reconstruction in a neural network.
Vietoris-Rips: A filtration captures how topological features (like clusters, loops, voids) appear and disappear as the scale changes. This persistence is visualized in barcodes or persistence diagrams. The Vietoris–Rips filtration is one of the most common constructions in TDA for extracting topological features from a point cloud.
📌 This article focuses on key concepts of Topological Deep Learning. Topological Data Analysis techniques will be explored in future articles.
Topological Deep Learning
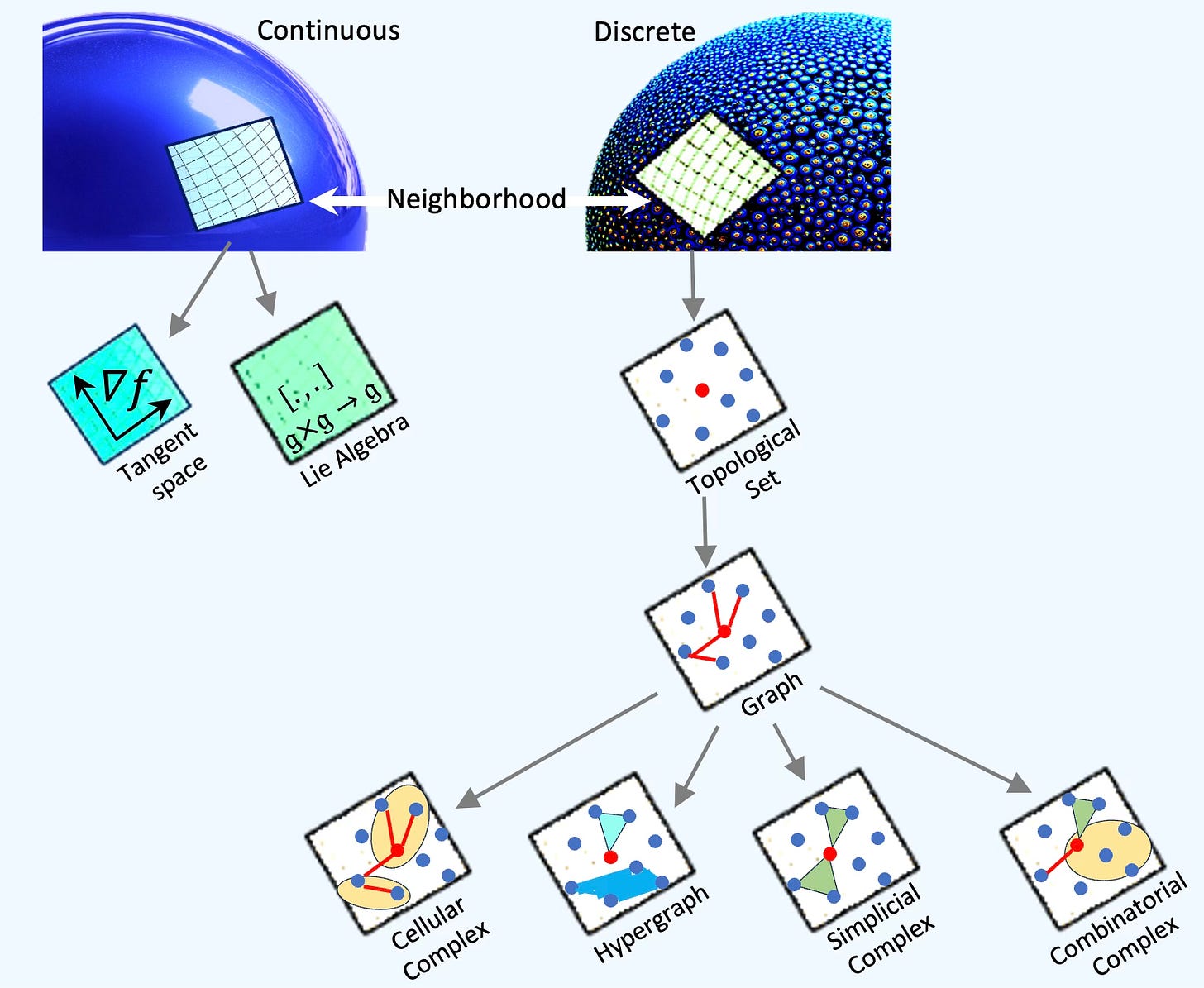
As previously noted, Topological Deep Learning (TDL) is a subfield of Geometric Deep Learning distinguished by the way it defines local neighborhoods.
In geometric models built on continuous manifolds, the neighborhood around a point is typically represented by a local Euclidean space—often formalized as a tangent space or the Lie algebra at the identity of the manifold.
In contrast, as illustrated below, TDL defines the neighborhood of a node (or embedded vector) as the collection of nodes it is topologically related to—whether through similarity, edges, simplices, or other higher-order connections [ref 7].
Fig. 3 Illustration of Difference Between GDL and TDL from the Perspective of Data Point/Feature/Node Neighborhood.
A point cloud has spatial coordinate (x, y, z) and features (real vector) but does not contain any information about how points are connected (edges, faces,).
A neighborhood of a data point in a point cloud can be modeled as a discrete set within a topological space.
By defining relationships among these elements, they can be represented as nodes in a graph connected by edges.
This graph structure can be extended to capture higher-order topological relationships, such as:
Faces (e.g., triangles, tetrahedra), forming a simplicial complex
Hyperedges, leading to a hypergraph
Disjoint unions of topological disks, yielding a cellular complex
Heterogeneous collections of shapes, resulting in a combinatorial complex.
Topological Neural Networks
Since Topological Neural Networks are built upon the foundations of Graph Neural Networks (GNNs), we begin with a brief overview of the core components and concepts underlying GNNs.
📌 Key topics such as homophily, sampling and aggregation strategies, and training methods for GNNs have been discussed in earlier articles [Ref 4, 5, 6]
GNN Revisited
A GNN is an optimizable transformation on all attributes of the graph (nodes, edges, global context) that preserves graph symmetries (permutation invariances). GNN takes a graph as input and generate/predict a graph as output.
Data on manifolds can often be represented as a graph, where the manifold's local structure is approximated by connections between nearby points. GNNs and their variants (like Graph Convolutional Networks (GCNs) extend neural networks to process data on non-Euclidean domains by leveraging the graph structure, which may approximate the underlying manifold.
There are 3 types of tasks to be performed on a GNN:
Graph-level task that predicts the property of the entire graph such as classification problems.
Node-level task that predicts if a node belongs to a specific class or image segmentation or part of speech a word belongs to.
Edge-level task that predicts the relationship between nodes that can be classified (discovery of connections between entities or nodes.
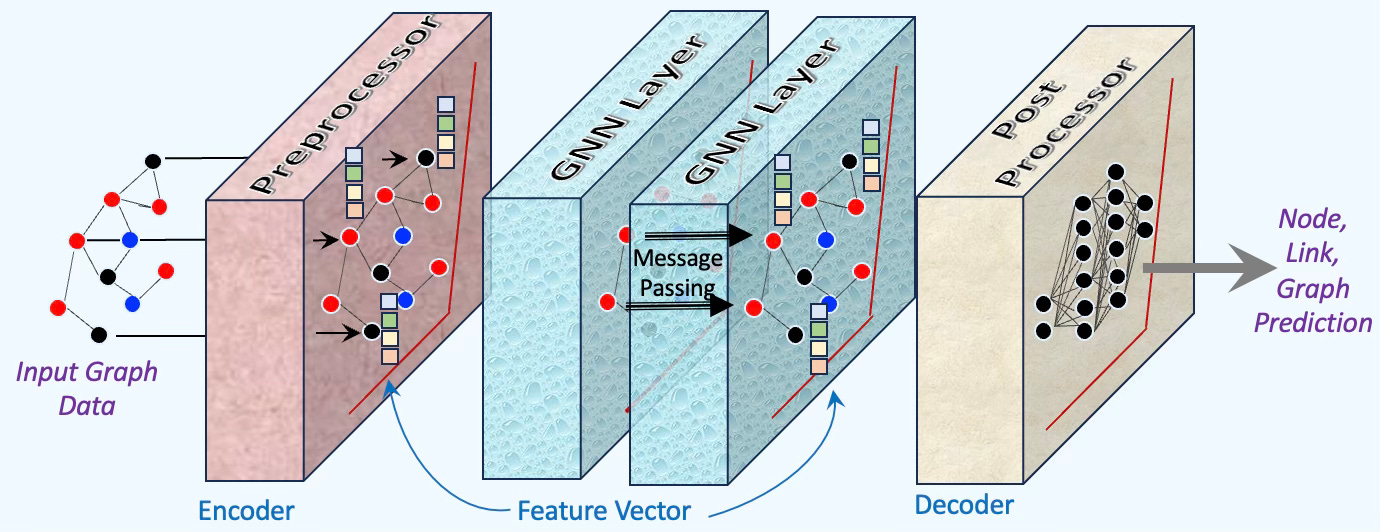
There are three groups of layers
Pre-processing layers: Feedforward layers that encode the node data into vector features for each node.
Message-passing layers: Execute the message passing and aggregation at each layer.
Post-processing layers: Feedforward layers decoding the output of the Message passing layers and predict node, link or graph.
Fig. 4. Illustration of Pre/Post Processing, Neural Layers and Message Passing for Graph Neural Networks
Each layer of a Graph Neural Network (GNN) performs a message passing operation, followed by an aggregation (often a summation) step [ref 7]. The specific design of these two components—how messages are exchanged and aggregated—determines the overall architecture of the GNN, ranging from simple to more sophisticated forms, such as:
Convolutional GNNs
Attention-based GNNs
Generic message-passing GNNs
Topological Networks Architecture
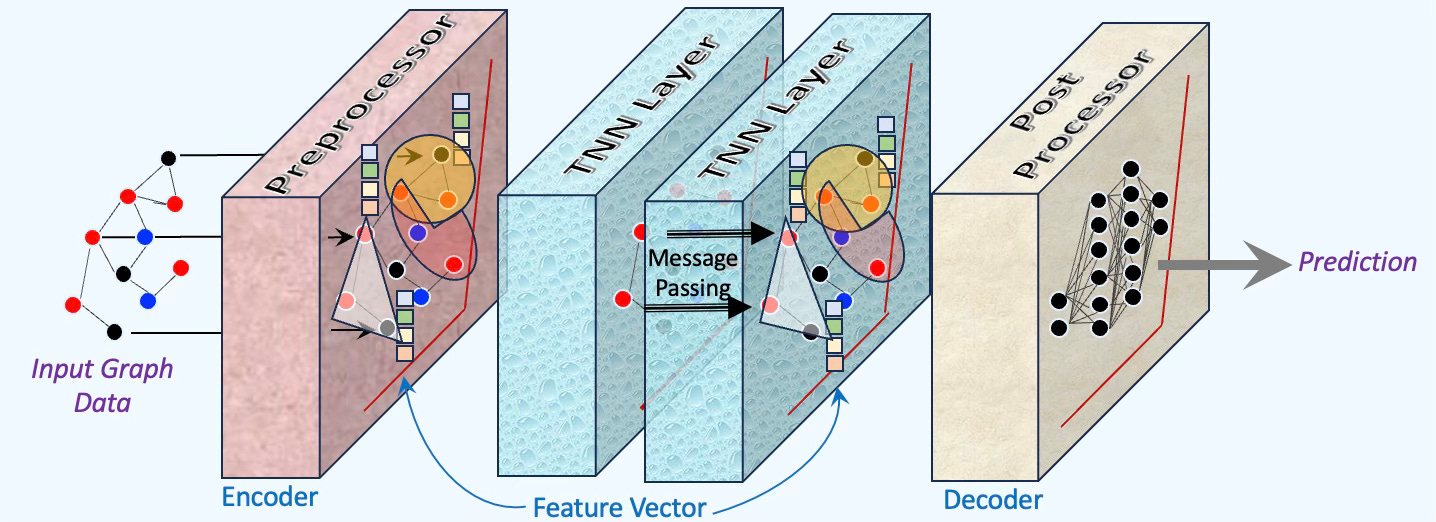
Given the conceptual parallels between graph networks and topological domains, it is natural to build upon established architectures and tools originally developed for graph-based classification and regression tasks [ref 8]
However, several key distinctions arise:
Encoding: The encoder must generate embeddings not only for nodes, but also for higher-order topological structures such as simplicial complexes or hypergraphs.
Message Passing: Unlike standard GNNs where message passing occurs between neighboring nodes, topological models must extend this mechanism to operate over both nodes and higher-dimensional topological entities.
Fig. 5 Illustration of pre/post processing and Topological Neural Layers
Messages Aggregation
In graph neural networks, aggregation typically involves collecting messages from immediate node neighbors. In contrast, topological neural networks introduce a two-tiered aggregation process:
Intra-neighborhood aggregation among nodes
Inter-neighborhood aggregation across topological domains (e.g., faces, hyperedges, or cells)
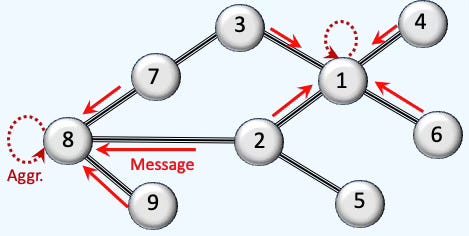
📌 For convenience, we arbitrarily assign node indices starting at 1. This convention is followed for all the articles related to Topological Deep Learning.
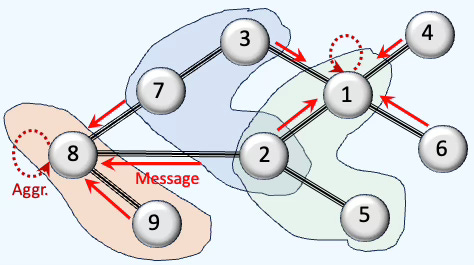
To set the stage, we first review the standard message-passing and aggregation process in Graph Neural Networks.
Fig. 6 Illustration Message-passing and Aggregation in Graph Neural Networks
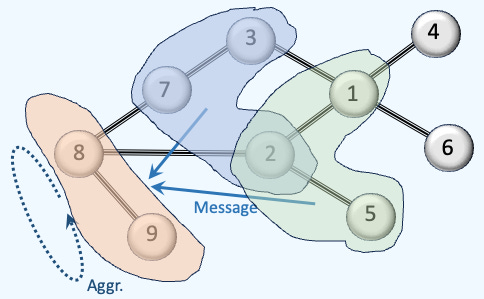
The message passing and aggregation process is similarly carried out within each topological domain, such as a simplicial complex, as illustrated below:
Fig. 7 Illustration Intra-neighborhood Message-Passing and Aggregation in TDL
Finally, the messages from each higher-order domain are processed and aggregated.
Fig. 8 Illustration Inter-neighborhood Message-Passing and Aggregation in TDL
As you can see, Topological Neural Networks are not vastly different from Graph Neural Networks.
📚 Libraries
This newsletter prides itself to provide its reader with hands-on experience with various topics. Therefore, this article won’t be complete without a review of the important Python tools and libraries supporting TDL.
NetworkX
NetworkX is a BSD-license powerful and flexible Python library for the creation, manipulation, and analysis of complex networks and graphs. It supports various types of graphs, including undirected, directed, and multi-graphs, allowing users to model relationships and structures efficiently [ref 9 & 10]
NetworkX provides a wide range of algorithms for graph theory and network analysis, such as shortest paths, clustering, centrality measures, and more. It is designed to handle graphs with millions of nodes and edges, making it suitable for applications in social networks, biology, transportation systems, and other domains. With its intuitive API and rich visualization capabilities, NetworkX is an essential tool for researchers and developers working with network data.
The library supports many standard graph algorithms such as clustering, link analysis, minimum spanning tree, shortest path, cliques, coloring, cuts, Erdos-Renyi or graph polynomial.
Installation
pip install networkxTopoX
TopoX equips scientists and engineers with tools to build, manipulate, and analyze topological domains—such as cellular complexes, simplicial complexes, hypergraphs, and combinatorial structures—and to design advanced neural networks that leverage these topological components.
The two packages we will leverage in future articles are
🔹 TopoNetX
An API for exploring relational data and modeling topological structures [ref 11]. It includes:
Atoms: Classes representing basic topological entities (e.g., cells, simplices)
Complexes: Classes for constructing and working with simplicial, cellular, path, and combinatorial complexes, as well as hypergraphs
Reports: Tools for inspecting and describing atoms and complexes
Algorithms: Utilities for computing adjacency and incidence matrices, and various Laplacian operators
Generators: Functions for creating synthetic topological structures
Installation
pip install toponetx🔹 TopoModelX
A library that provides template implementations for Topological Neural Networks. It supports applying convolution, message passing, and aggregation operations over topological domains [ref 12].
Installation
pip install topomodelxGudhi
The GUDHI (Geometry Understanding in Higher Dimensions) library is an open-source framework focused on Topological Data Analysis (TDA), with a particular emphasis on understanding high-dimensional geometry.
Similar to TopoX, it equips researchers with tools to construct and manipulate various complexes, including simplicial, cell, cubical, Alpha, and Rips complexes.
GUDHI supports the creation of filtrations and the computation of topological descriptors such as persistent homology and cohomology. Additionally, it offers functionality for processing and transforming point cloud data.
Installation
pip install gudhi🧠 Key Takeaways
✅ TDA analyze shape of data while TDL is used to build linear models using topological spaces
✅ TDL is a subset of Geometric Deep Learning and extends traditional machine learning with shape analysis and extraction of topological features
✅ List of Topological spaces includes Topological sets, graphs, simplicial, cellular and combinatorial complexes as well as hypergraphs
✅ Topological Neural Networks extend Graph Neural Networks by adding topological structure (e.g., complexes) and signals to the list of existing features and adapting message-passing and aggregation scheme.
✅ TopoX, NetworkX and Gudhi are open-source libraries critical to the investigation of TDA and TDL.
📘 References
Introduction to Geometric Deep Learning: Topological Data Analysis P. Nicolas - Hands-on Geometric Deep learning
Introduction to Geometric Deep Learning P. Nicolas - Hands-on Geometric Deep learning
A Comprehensive Introduction to Graph Neural Networks - Datacamp
Topological Deep Learning: Going Beyond Graph Data M. Hajij et all
Architectures of Topological Deep Learning: A Survey on Topological Neural Networks M. Papillon, S. Sanborn, M. Hajij, N. Miolane
Visualization of Graph Neural Networks P. Nicolas - LinkedIn Newsletter
TopoNetX Documentation - PyT-Team
TopoModelX Documentation - PyT-Team
🛠️ Exercises
👉 Since this article does not contain any source code, this section is dedicated to quizzes.
Q1: What additional inputs does a topological neural model require beyond the features extracted from the input data?
Q2: How does message aggregation in Topological Deep Learning (TDL) differ from that in Graph Neural Networks (GNNs)?
Q3: Which topological domains are most commonly used in Topological Data Analysis (TDA) and Topological Deep Learning (TDL)?
Q4: In what way does TDL differ from Geometric Deep Learning (GDL) with respect to transformation invariance?
Q5: What do Betti numbers quantify in a topological space?
Q6: How do adjacency and incidence matrices differ in representing graph or topological structures?
👉 Answers
💬 News & Reviews
This section focuses on news and reviews of papers pertaining to geometric deep learning and its related disciplines.
Paper Review: Topological Deep Learning: Going Beyond Graph M. Hajij, et all.
Exploring non-Euclidean datasets but finding Graph Neural Networks (GNNs) limiting?
This comprehensive paper offers an excellent introduction to Topological Deep Learning (TDL). It begins with a clear definition of TDL, an extensive glossary, and a detailed discussion of the advantages of using topological structures for modeling heterogeneous data in machine learning.
Through intuitive examples, the authors show how relational and domain-based data can be enriched by augmenting graphs and meshes with higher-order relations—such as cells—capturing more complex structures.
The core focus lies on simplicial, combinatorial, and cell complexes, culminating in hypergraphs as expressive tools for modeling higher-order interactions. These structures provide a natural extension to GNNs, complementing message-passing and pooling operations with geometric symmetries, invariance, and equivariance.
The paper delves into the algebraic and structural foundations of combinatorial complexes, covering homomorphisms, pooling mechanisms, neighborhood operators, and associated matrix representations. It then introduces Combinatorial Complex Neural Networks for rank < 4, illustrating classification and prediction tasks within these structures.
A key contribution is the introduction of a push-forward operator—distinct from the differential geometry concept—which generalizes permutation-invariant aggregation to complex-based learning.
The paper concludes by surveying tools and libraries for TDL, including TopoNetX, and provides datasets to facilitate experimentation in this emerging area of AI.
Patrick Nicolas has over 25 years of experience in software and data engineering, architecture design and end-to-end deployment and support with extensive knowledge in machine learning.
He has been director of data engineering at Aideo Technologies since 2017 and he is the author of "Scala for Machine Learning", Packt Publishing ISBN 978-1-78712-238-3 and Geometric Learning in Python Newsletter on LinkedIn.