Introduction to Geometric Deep Learning
Facing challenges with high-dimensional, densely packed but limited data, and complex distributions? Geometric Deep Learning (GDL) offers a solution by enabling data scientists to grasp the true shape and distribution of data. This newsletter explores the diverse techniques and frameworks shaping the field of Geometric Deep Learning.
Table of Contents
🎯 Why this Matters
Purpose: Introduction to Geometric Deep Learning and how it addresses the limitations of current machine learning models.
Audience: Anyone with some basic understandings of artificial intelligence and machine learning.
Value: Learning about Geometric Deep Learning and Graph Neural Networks unlocks the ability to model complex, structured, and relational data, enabling advanced problem-solving in areas like social networks, molecular science, design optimization, and transportation systems.
⚠️ Limitations of Current Models
Deep Learning
Data scientists face challenges when building deep learning models that can be addressed by geometric, non-Euclidean representation of data. Those challenges are [ref 1]:
High dimensionality: Models related to computer vision or images deal with high-dimensional data, such as images or videos, which can make training more difficult due to the curse of dimensionality.
Availability of quality data: The quality and quantity of training data significantly affect the model's ability to generate realistic samples. Insufficient or biased data can lead to overfitting or poor generalization.
Underfitting or overfitting: Balancing the model's ability to generalize well while avoiding overfitting to the training data is a critical challenge. Models that overfit may generate high-quality outputs that are too similar to the training data, lacking novelty.
Embedding physics law or geometric constraints: Incorporating domain constraints such as boundary conditions or differential equations model s very challenging for high-dimensional data.
Representation dependence: The performance of many learning algorithms is very sensitive to the choice of representation (i.e. z-normalization impact on predictors).
Generative Models
Generative modeling includes techniques such as auto-encoders, generative adversarial networks (GANs), Markov chains, transformers, and their various derivatives.
Creating generative models presents several specific challenges beyond plain vanilla deep learning models for data scientists and engineers, primarily due to the complexity of modeling and generating data that accurately reflects real-world distributions [ref 2]. The challenges that can be addressed with differential geometry include:
Performance evaluation: Unlike supervised learning models, assessing the performance of generative models is not straightforward. Traditional metrics like accuracy do not apply, leading to the development of alternative metrics such as the Frechet Inception Distance (FID) or Inception Score, which have their limitations.
Latent space interpretability: Understanding and interpreting the latent space of generative models, where the model learns a compressed representation of the data, can be challenging but is crucial for controlling and improving the generation process.
💡 What is Geometric Deep Learning
Geometric Deep Learning has been introduced by M. Bronstein, J. Bruna, Y. LeCun, A. Szlam and P. Vandergheynst in 2017 [ref 3]. Readers can explore the topic further through a tutorial by M. Bronstein [ref 4].
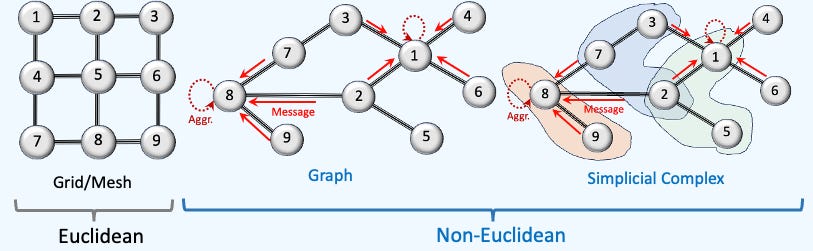
Geometric Deep Learning (GDL) is a branch of machine learning dedicated to extending deep learning techniques to non-Euclidean data structures. Currently, there is no universally agreed-upon, well defined scope for Geometric Deep Learning, as its interpretation varies among authors.
Here's a somewhat arbitrary breakdown:
Graphs: Represent relationships between entities (nodes/vertices and edges), such as social networks, knowledge graphs, and molecular structures. Graph Neural Networks (GNNs) are widely used models that leverage graph-based representations.
Topological Domains: Encode higher-level relationships between entities in scientific datasets using structures like hypergraphs, simplicial complexes, or cell complexes. Topological Data Analysis (TDA) and Topological Deep Learning address limitations of Graph Neural Networks by capturing non-local properties and dependencies.
Manifolds: Utilize differential and Riemannian geometry to represent low-dimensional, continuous, curved spaces or embeddings within higher-dimensional Euclidean spaces. Manifold learning and manifold neural networks are designed to extract intrinsic data representations.
Point Clouds: Represent 3D data often processed through mesh-based or grid-based models, enabling effective analysis of spatial structures.
Graph Neural Networks
Data on manifolds can often be represented as a graph, where the manifold's local structure is approximated by connections between nearby points. GNNs and their variants (like Graph Convolutional Networks (GCNs)) extend neural networks to process data on non-Euclidean domains by leveraging the graph structure, which may approximate the underlying manifold [ref 5, 6, 7]
Types of Graph Neural Networks
Graph Convolutional Networks (GCNs): GCNs generalize the concept of convolution from grids (e.g., images) to graphs. They aggregate information from a node's neighbors using normalized adjacency matrices and apply transformations to learn node embeddings.
Graph Attention Networks (GATs): GATs use attention mechanisms to learn the importance of neighboring nodes dynamically. Each edge is assigned a learned weight during aggregation.
GraphSAGE (Graph Sample and Aggregate):It learns node embeddings by sampling and aggregating features from a fixed-size neighborhood of each node, enabling scalable learning on large graphs.
Graph Isomorphism Networks (GINs): GINs are designed to be as powerful as the Weisfeiler-Lehman (WL) graph isomorphism test, distinguishing graph structures more effectively.
Spectral Graph Neural Networks (SGNN): These networks operate in the spectral domain using the graph Laplacian. They use eigenvectors of the Laplacian for convolution-like operations.
Graph Pooling Networks: They summarize graph information into a smaller representation, similar to pooling in CNNs. They can be categorized into Global and hierarchical pooling
Hyperbolic Graph Neural Networks: These networks operate in hyperbolic space, which is well-suited for representing hierarchical or tree-like graph structures.
Dynamic Graph Neural Networks: These networks are designed to handle temporal graphs, where nodes and edges evolve over time.
Relational Graph Convolutional Networks (R-GCNs):R-GCNs extend GCNs to handle heterogeneous graphs with different types of nodes and edges.
Graph Transformers: They adapt the Transformer architecture to graph-structured data using attention mechanisms and global context.
Graph Autoencoders: These are used for unsupervised learning on graphs, aiming to reconstruct graph structure and node features.
Diffusion-Based GNNs: These networks use graph diffusion processes to propagate information.
PyTorch Geometric [ ref 8] is a widely used library for implementing, training, and evaluating Graph Neural Networks. This library will be discussed in a future article.
📌 Future articles will cover Graph Neural Network architecture and theory, along with hands-on applications implemented using Torch Geometric.
Topology
Topological Data Analysis
Topological Data Analysis (TDA) is a methodology that applies concepts from algebraic topology and computational geometry to analyze and extract meaningful patterns from complex datasets. It provides a geometric and topological perspective to study the shape and structure of data. TDA seeks to develop rigorous mathematical, statistical, and algorithmic techniques to infer, analyze, and leverage the intricate topological and geometric structures underlying data, often represented as point clouds in Euclidean or more general metric spaces. [ref 9].
The most common topological domains are
Simplicial Complexes
Cellular Complexes
Hypergraphs
Combinatorial Complexes
You may wonder where any of these topological domains fits in the overall picture of data representation, including graph and grids.
Features
Understand data shape: TDA focuses on capturing the "shape" or structure of data, including patterns, clusters, loops, and voids that traditional methods might miss.
Reduce dimension: It enables the extraction of features that summarize the global properties of high-dimensional data while preserving important topological characteristics.
Discount noise: TDA methods are designed to distinguish signal from noise effectively, providing stable and meaningful insights even in noisy datasets.
Quantify global properties: TDA quantifies global and intrinsic properties of datasets, such as connectedness, holes, or higher-dimensional features.
Benefits
Insight into Complex Structures: TDA can reveal features like clusters, loops, and voids in data that are not immediately apparent using standard statistical or machine learning techniques.
Versatility: It can be applied to any dataset, regardless of the domain, and works effectively on structured, unstructured, and graph-based data.
Improved Noise Tolerance: Topological features are stable and robust to small perturbations in data, making TDA especially valuable for noisy or incomplete datasets.
Enhancing Machine Learning: TDA features can be combined with machine learning models to improve predictions, clustering, and classification, especially in tasks where geometry and relationships between data points matter.
Nonlinearity Detection: TDA captures nonlinear patterns and relationships that may be missed by linear methods like PCA or linear regression.
Recently, TDA has evolved into Topology Deep Learning that encompasses extracting high level abstraction and hierarchical representation from data. For instance, Topological neural networks enable the processing of data, for example via higher-order message-passing schemes on a topological space [ref 10].
📌 The most common data structures and algorithms for TDA as implemented in GUDHI library, with C++ implementation and Python interfaces [ref 11].
Topological Deep Learning
Topological Deep Learning (TDL) is an emerging area of machine learning that extends traditional deep learning and graph neural networks (GNNs) to operate on higher-order topological structures beyond simple graphs. While GNNs model pairwise relationships (nodes and edges), TDL leverages the mathematics of algebraic topology to capture multi-way interactions (e.g., triangles, tetrahedra) and topological invariants like holes, cycles, and cavities.
TDL is widely considered a subfield of Geometric Deep Learning (GDL). Deep Learning distinguished by the way it defines local neighborhoods.
In geometric models built on continuous manifolds, the neighborhood around a point is typically represented by a local Euclidean space—often formalized as a tangent space or the Lie algebra at the identity of the manifold.
The most common applications of TDL are:
Molecular and protein modeling (capturing 3D binding pockets, loops).
Mesh and 3D object analysis (e.g., shape classification, segmentation).
Sensor and communication networks (detecting coverage holes and cycles).
Neuroscience (studying brain connectivity and functional cycles).
Point cloud data (capturing geometric and topological invariants).
Complex social and financial networks (analyzing group interactions).
Data Manifolds
Machine learning models based on manifolds leverage differential geometry [ref 12]. A manifold is essentially a space that, around every point, looks like Euclidean space, created from a collection of maps (or charts) called an atlas, which belongs to Euclidean space. Differential (or smooth) manifolds have a tangent space at each point, consisting of vectors. Riemannian manifolds are a type of differential manifold equipped with a metric to measure curvature, gradient, and divergence [ref 13].
In deep learning, the manifolds of interest are typically Riemannian due to these properties.
It is important to keep in mind that the goal of any machine learning or deep learning model is to predict p(y) from p(y|x) for observed features y given latent features x.
The latent space x can be defined as a differential manifold embedding in the data space (number of features of the input data).
Given a differentiable function f on a domain a manifold M of dimension d is defined by:
In a Riemannian manifold, the metric can be used to
Estimate kernel density
Approximate the encoder function of an auto-encoder
Represent the vector space defined by classes/labels in a classifier
Studying data that reside on manifolds can often be done without the need for Riemannian Geometry, yet opting to perform data analysis on manifolds presents three key advantages:
By analyzing data directly on its residing manifold, you can simplify the system by reducing its degrees of freedom. This simplification not only makes calculations easier but also results in findings that are more straightforward to understand and interpret.
Understanding the specific manifold to which a dataset belongs enhances your comprehension of how the data evolves over time.
Being aware of the manifold on which a dataset exists enhances your ability to predict future data points. This knowledge allows for more effective signal extraction from datasets that are either noisy or contain limited data points.
Geomstats [ref 14] and PyTorch Geometric [ref 8] are among the most widely used Python libraries for machine learning on data manifolds.
📌 Future articles will cover topics such as application of differential geometry, deep learning models on manifolds along with hands-on applications and information geometry.
Mesh & Grid Based Models
These models are a special cases of Graph Neural Networks and Geometric Deep Learning applied to 3D spaces.
A mesh is a collection of vertices, edges, and faces that define the shape of a 3D object. Mesh-based learning focuses on directly processing these structures. A grid represents data in a structured, regular manner, such as a 2D/3D pixel or voxel grid.
Mesh-based learning models use triangular, quadrilateral, or polygonal meshes to represent surfaces. It preserves topology and local geometric structure and ideal for irregular surfaces, such as 3D scans, medical imaging, and CAD models [ref 15].
The common designs are
GNN on meshes for which mesh is treated as a graph
Spectral models that use the Laplacian of the mesh
Geometric Deep Learning methods that apply message passing the mesh.
A grid represents data in a structured, regular manner, such as a 2D/3D pixel or voxel grid. It uses uniform grids and is suitable for applications where data is naturally aligned with a regular grid.
The common designs are
Voxel-based Neural Networks converting 3D objects into voxel grids and applies 3D CNNs.
Implicit Representations representing surfaces as signed distance functions
Physics-Based Learning simulating physical interactions within a grid.
📈 Applications
Classifying applications based on their association with specific models can be challenging, as multiple approaches may offer accurate representations and reliable predictions. Here are some examples:
Community detection: Identify clusters or communities in social networks (Graph Neural Networks).
Recommendations: Suggest products, services or connection using graph-based similarity (Graph Neural Networks).
Drug Discovery: Predict molecular properties, drug-target interactions, or generate novel compounds (Graph Neural Networks).
Protein Structure Prediction: Model amino acid interactions to predict 3D protein folding and stability (Graph Neural Networks).
Gene Networks: Analyze gene regulatory interactions or detect disease pathways (Graph Neural Networks).
3D Shape Analysis: Analyze and process point clouds or 3D meshes (3D Mesh model),
Action Recognition: Use graphs to model relationships between body joints or objects in video sequences (Graph Neural Networks).
Fraud Detection: Detect fraudulent activities by modeling transaction networks (Graph Neural Networks).
Portfolio Optimization: Represent and analyze stock correlations using graphs (Graph Neural Networks).
Electronic Circuit Design: Optimize circuit layouts represented as graphs (Graph Neural Networks).
Risk Management: Model credit risk and customer relationships in financial networks (Graph Neural Networks).
Disease Prediction: Model patient similarities and interactions for personalized medicine (Graph Neural Networks).
Patient Care Networks: Represent patient-doctor or hospital networks to optimize care pathways (Graph Neural Networks).
Drug Repurposing: Identify new therapeutic uses for existing drugs using graph-based analysis (Graph Neural Networks).
Physics-Informed Learning: Modeling physical systems using graphs and manifolds (Manifold learning).
Disease Prediction: Model patient similarities and interactions for personalized medicine (Graph Neural Networks).
Patient Care Networks: Represent patient-doctor or hospital networks to optimize care pathways (Graph Neural Networks).
Drug Repurposing: Identify new therapeutic uses for existing drugs using graph-based analysis (Graph Neural Networks).
Knowledge Graphs: Improve semantic search, question answering, and reasoning by embedding nodes and edges (Graph Neural Networks).
Collaboration Networks: Model co-authorship or citation networks for analyzing research trends (Graph Neural Networks).
Astronomy: Analyze large-scale cosmic networks and galaxy clusters (Graph Neural Networks).
Power Grid Management: Monitor and optimize energy distribution networks (Graph Neural Networks).
Text Classification: Represent relationships between words, sentences, or documents as graphs for classification (Graph Neural Networks).
Trajectory Optimization: Manifold learning helps model and optimize robot trajectories, especially in constrained spaces like joints or environments (Manifold learning).
Pose Estimation: Manifold models are used to represent rotations, translations, and orientations in 3D space (e.g., SO(3), SE(3) groups) (Manifold learning).
3D Shape Analysis: Used for shape recognition, segmentation, and alignment (Manifold learning).
Physics Simulations: Manifolds represent physical systems like fluid dynamics or electromagnetic fields for improved simulation and understanding (Manifold learning).
Manifold-based Data Augmentation: Generative models use learned manifolds to create augmented data samples that adhere to the original data distribution (Manifold learning).
Brain Signal Analysis: EEG/MEG data is modeled on manifolds to uncover latent patterns related to neurological states (Manifold learning).
Matrix Factorization: Manifold-based optimization is applied to problems like low-rank matrix approximation in recommendation systems (Manifold learning).
Topology and Geometry Analysis: Persistent homology and topological data analysis rely on manifold representations for analyzing complex data structures (Topological data analysis).
Manifold-Aware Transformers: Emerging methods adapt transformer architectures to manifold-structured data (Topological data analysis).
Hyperbolic Embeddings: Effective for modeling hierarchical or tree-like data structures (e.g., taxonomies, organizational hierarchies) (Topological data analysis).
⚙️ Frameworks & Libraries
There are numerous open-source Python libraries available, with a variety of focuses not exclusively tied to machine learning or generative modeling:
diffgeom: A PyPi project aimed at symbolic differential geometry. Detailed information is available at PyPi Diffgeom.
SymPy: A more comprehensive library for symbolic mathematics, useful for studying topology and differential geometry. Documentation is accessible at SymPy
Geomstats: Designed for performing computations and statistical analysis on nonlinear (Riemannian) manifolds (Github Geomstats).
PyG: PyTorch Geometric is a library built on PyTorch dedicated to geometric deep learning and graph neural networks (Pytorch Geometric).
PyRiemann: A package based on scikit-learn provides a high-level interface for processing and classification of multivariate data through the Riemannian geometry of symmetric positive definite matrices (pyRiemann: Machine learning for multivariate data with Riemannian geometry).
PyManOpt: A library for optimization and automatic differentiation on Riemannian manifolds (PyManOpt).
GUDHI: The library is a generic open source C++ library with a Python interface for Topological Data Analysis and Higher Dimensional Geometry Understanding (GUDHI - Geometry Understanding in Higher Dimensions).
TopoX: TopoX are a set of Python packages for meeting diverse computational needs on topological domains. Topological domains are the natural mathematical structures representing relations between the components of a dataset (TopoX Documentation)
🧠 Key Takeaways
✅ Geometric Deep Learning (GDL) tackles key limitations of traditional deep learning models, including overfitting, representation dependency, and interpretability challenges.
✅ GDL methods fall into several categories: Graph Neural Networks, Topological Data Analysis, data manifold models, and mesh/grid-based models.
✅ Applications leveraging GDL are beginning to emerge, supported by various Python libraries, with Geomstats and PyTorch Geometric being among the most widely used.
✅ This newsletter explores the diverse techniques and frameworks shaping the field of Geometric Deep Learning.
📘 References
Limitations of Deep Neural Networks - S. Tsimenidis
Geometric and spectral limitations in generative adversarial networks - Rutgers University
Geometric foundations of Deep Learning - M. Bronstein
A Comprehensive Introduction to Graph Neural Networks - Datacamp
An introduction to Topological Data Analysis: fundamental and practical aspects for data scientist - F. Chazal, B. Michel
Position: Topological Deep Learning is the New Frontier for Relational Learning
Differential geometry for machine learning - R. Grosse
Differential geometry for generative modeling - S. Hauberg
🛠️ Exercises
Q1: What are the two most widely used Python libraries for Geometric Deep Learning?
Q2: Can you name four different types of Graph Neural Networks?
Q3: What are the advantages of using Topological Data Analysis?
Q4: How does a differential (smooth) manifold differ from a Riemannian manifold?
Q5: Between mesh-based and grid-based learning models, which has the higher computational cost?
👉 Answers
💬 News & Reviews
This section focuses on news and reviews of papers pertaining to geometric deep learning and its related disciplines.
Paper review Intrinsic and extrinsic deep learning on manifolds Y. Fang, i. Ohh, V. Gupta, L. Lin 2023
This paper introduces two types of general deep neural network architecture on manifolds:
Extrinsic deep neural network on manifolds
This architecture maintains the geometric characteristics of manifolds by employing an equivariant embeddings of a manifold into the Euclidean space.
This method is applied in regression models or Gaussian processes on manifolds, where the idea is to construct the neural network based on the manifold's representation after embedding, while still maintaining its geometric properties. By adopting this strategy, it becomes possible to utilize stochastic gradient descent and backpropagation techniques from Euclidean space. This results in enhanced accuracy compared to conventional machine learning algorithms like SVM, random forest, etc.
Intrinsic deep neural network on manifolds
The objective is to embed the inherent geometric nature of Riemannian manifolds using exponential and logarithmic maps. This framework, which projects localized points from a Riemannian manifold onto a single tangent space, proves beneficial when embeddings cannot be determined. Each localized tangent space (or chart) is mapped (via exp/log functions) onto a neural network. This architectural approach achieves higher accuracy compared to deep models in Euclidean space and the Extrinsic architecture.
These two frameworks are assessed based on their performance in
Classifying health-related simulated datasets on a spherical manifold
Dealing with symmetric semi-positive definite matrices.
Patrick Nicolas has over 25 years of experience in software and data engineering, architecture design and end-to-end deployment and support with extensive knowledge in machine learning.
He has been director of data engineering at Aideo Technologies since 2017 and he is the author of "Scala for Machine Learning", Packt Publishing ISBN 978-1-78712-238-3 and Geometric Learning in Python Newsletter on LinkedIn.