A Journey into the Lie Group SO(4)
Interested in exploring Special Orthogonal Groups beyond SO(3)? This article delves into the 6-dimensional SO(4) group and its associated Lie algebra.
Table of Contents
🎯 Why this matters
Purpose: While not as widely used as the SO(3) group, SO(4) has found valuable applications in fields such as biology, chemistry, and Geometric Deep Learning. This article offers a different perspective on rotation groups.
Audience: Data scientists and engineers working on complex modeling—such as equivariant neural networks, protein folding, or those simply curious about rotation groups beyond SO(3)—may find this topic particularly insightful
Value: Learn how to extend Geomstats functionality to support operations on SO(4) group.
🎨 Modeling & Design Principles
⚠️ A thorough tutorial and explanation of Lie groups, Lie algebras, and geometric priors for deep learning models is beyond the scope of this article. Instead, the following sections concentrate on experiments involving key elements and operations on Lie groups using the Geomstats Python library.
Special Orthogonal Groups
📌 Smooth manifolds and Lie groups have been introduced and put in practice in previous articles of this newsletter [ref 1, 2 & 3]
The Special Orthogonal n-dimensional Groups SO(n) are the Lie groups that represents rotations in n-dimensional space. It is widely used in robotics, physics, computer vision, and geometric deep learning to describe rigid body rotations without scaling or reflection.
[1] Enforces orthogonally for which the unit of rotations are mutually perpendicular. It is equivalent to O(n) group.
[2] Ensures rotation and preserves orientation.
SO4 Group & Algebra
The SO(4) Lie group—the group of all 4×4 orthogonal matrices with determinant 1—describes rotations in 4-dimensional Euclidean space. It has several interesting properties and applications across mathematics, physics, and geometric deep learning.
A SO(4) group element has 6 dimensions:
Here are some of its applications
Differential Geometry & Topology
SO(4) acts as the rotation group of the tangent spaces of a 4-manifold, useful in:
Studying curvature tensors (e.g., decomposition of the Riemann tensor).
Constructing frame bundles or principal bundles.
Geometric Deep Learning
Equivariant neural networks use SO(n) symmetries, including SO(4), to build models invariant to 4D rotations (e.g., in processing 4D data like spatio-temporal signals or hyperspherical embeddings).
In protein folding, 4D transformations are sometimes used in intermediate representations or high-dimensional embeddings of spatial structures.
Biology & Chemistry
SO(4) symmetry may arise in the modeling of conformational spaces of molecules or proteins, where rotation in high-dimensional abstract space reflects complex structural flexibility.
SO4 is a 6-dimensional group (same as SO(3) × SO(3)), decomposable into self-dual and anti-self-dual components [ref 4].
SO4 self-dual matrices
SO4 self-anti-dual matrices
Exponential & Logarithm Maps
The exponential and logarithm maps have key components of a smooth manifolds (ref 1, 2). We already described the exponential and logarithm maps for Special Orthogonal Group in a previous article.
Exponential maps a Lie algebra element (skew-symmetric matrix) to a Lie group element (orthogonal matrix with det = 1). Given a SO4 algebra A:
The logarithm maps a 4-dimensional rotation R matrix to the Lie algebra as:
⚠️ The Rodrigues’s rotation formula defined in a previous article Rodrigues's Formula, does not directly apply to Lie algebras so(n) for n > 3. It is a closed-form expression for the exponential of a skew-symmetric matrix for the Lie algebra so(3) which is isomorphic to 3-dimensional Euclidean space [ref 5]
Operations
The inverse of a rotation matrix SO(4) is equal to its transpose.
The composition of SO(4) refers to the successive application of rotations represented by these matrices (a.k.a. matrix multiplication). This composition is also associative, meaning the way you group the multiplications doesn't change the result although the order of operations matters (right-to-left).
For two groups f, g and two 4-dimensional matrices F, G on the Lie Algebra
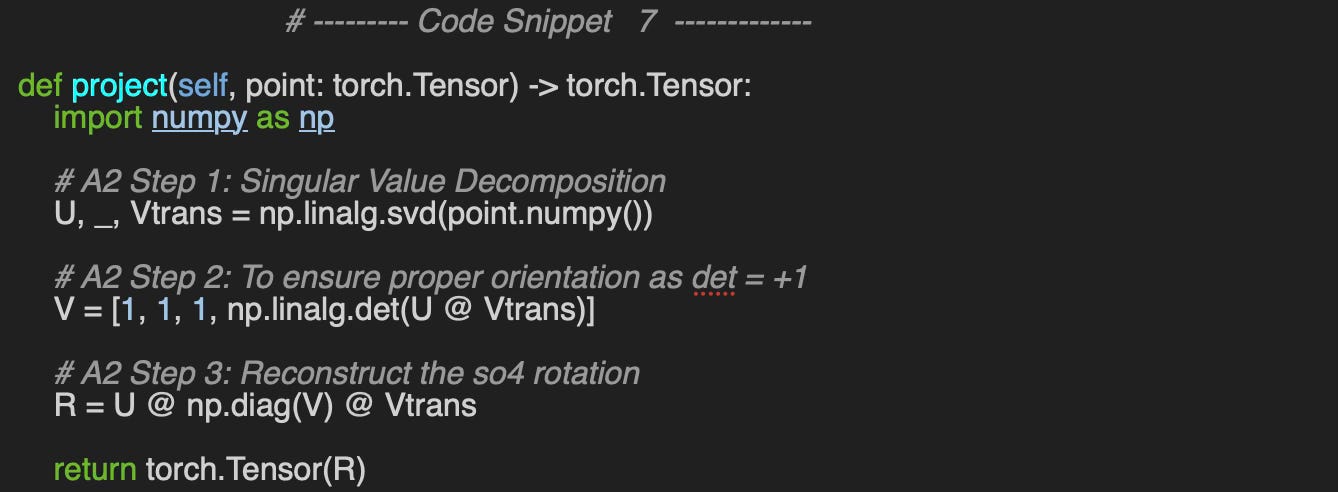
The projection of a matrix onto SO(4) refers to finding the closest matrix R in SO(4) to a given 4 x 4 matrix of real values M, typically one that is not exactly a valid rotation matrix due to noise or numerical errors.
The problem is solved using the Singular Value Decomposition of the input matrix M
📈 Visualization
Overview
Visualizing the Lie group SO(4) is inherently difficult due to its 6-dimensional structure. However, several techniques—from algebraic decompositions to lower-dimensional projections—can offer meaningful insights.
Examples include:
Algebraic decomposition of the Lie algebra so(4) into two independent so(3) components so(3) + so(3)
Projecting 4D geometric objects (such as hyperspheres or tesseracts) into 3D space for visualization.
Animating 4×4 rotation matrices, where SO(4) acts on 4D vectors, and the results are projected into 3D.
Visualizing elements of the Lie algebra so(4)so(4) as vector fields around the identity element.
Group decomposition of SO(4) into a product of simpler groups: SU(2)×SU(2), revealing deeper symmetry structure.
Decomposition into 3D rotations
The Lie decomposition of SO(4) is formally defined as
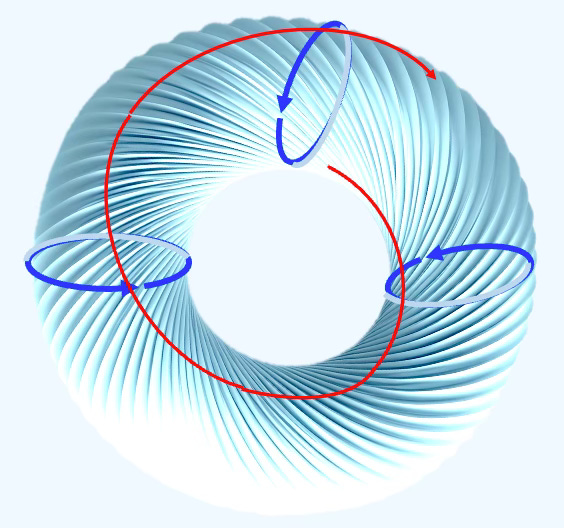
In a nutshell, each rotation in SO(4) group is a combination of two 3-dimensional rotations orthogonally over 2 planes. A simplistic visualization consists of animating the two 3D rotations in two separate coordinate planes such as {x, y} & [z, t} or {x, z} & {y, t},
Visualization of SO(4) using two 3D rotations on orthogonal planes
Animated 4D Hypersphere
The trick is to apply SO(4) transformation to an hypersphere and project these objects into 3D orthographically and animate their motion.
Visualization of SO(4) through animation of projection of an 4D hypersphere in 3D
⚠️ Lie groups do not resemble spheres or hyperspheres, but we use them here purely for illustrative purposes.
⚙️ Hands-on with Python
Environment
Libraries: Python 3.12.5, PyTorch 2.5.0, Numpy 2.2.0, Geomstats 2.8.0
Source code: Github.com/geometriclearning/geometry/lie/son_group.py
To enhance the readability of the algorithm implementations, we have omitted non-essential code elements like error checking, comments, exceptions, validation of class and method arguments, scoping qualifiers, and import statements.
Setup
📌 Many articles in this newsletter make use of PyTorch and PyTorch Geometric, so we adopt torch.Tensor as the primary type for representing elements of Lie groups and Lie algebras.
We leverage Geomstats library, an open-source Python package for computations, statistics, and machine learning on nonlinear manifolds, introduced in previous articles [ref 7, 8, 9].
Geomstats serves as a practical tool for gaining hands-on experience with geometric learning fundamentals while also supporting future research in the field. The Geomstats library is described in detail in the following article Exploring Geometric Learning with Geomstats of this newsletter.
We reuse the generic class SOnGroup introduced in a previous article [ref 6]
SO(4) Element Generation
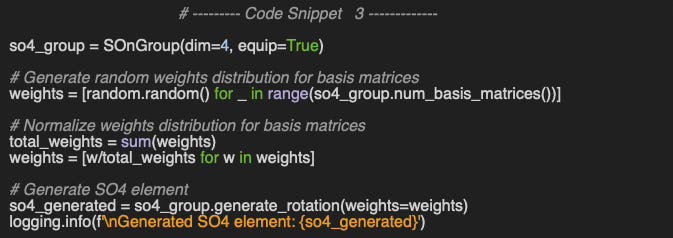
The previous article on Special Orthogonal Groups describes 4 different methods to generate so(n) Algebra elements [ref 10]. This section focuses on the generation of so4 matrices as a linear combination of weighted basis matrices implemented by the method generate_rotation (Code snippet 2).
We evaluate the method generate_rotation in generating a so4 elements as a linear combination of 6 randomly weighted basis matrices (Code snippet 3).
Output
Generated SO4 element:
[[ 0.0000, -0.1344, 0.1778, -0.3079],
[ 0.1344, 0.0000, -0.1703, -0.0675],
[-0.1778, 0.1703, 0.0000, -0.1421],
[ 0.3079, 0.0675, 0.1421, 0.0000]]The validation of rotation matrix belonging to the SO(4) group, is implemented by the method validation_points described in a previous article [ref 10].
Operations on SO(4)
Composition
As in the previous article with SO(2) and SO(3) groups, we evaluate
Composition of the two random rotation matrices
Composition of a random rotation with itself
Output
Rotation 1:
[[ 0.0771, 0.9473, 0.2911, -0.1097],
[ 0.4057, 0.2112, -0.8679, -0.1936],
[ 0.1428, 0.1370, -0.1170, 0.9732],
[ 0.8995, -0.1982, 0.3851, -0.0578]])
Rotation 2:
[[ 0.5067, 0.6421, 0.4879, 0.3049],
[ 0.3776, -0.3841, -0.3620, 0.7608],
[ 0.7735, -0.2721, -0.0921, -0.5650],
[ 0.0498, 0.6051, -0.7889, -0.0946]])
Composed Rotation:
[[ 0.6164, -0.4599, -0.2456, 0.5901],
[-0.3956, 0.2983, 0.3542, 0.7931],
[ 0.0821, 0.6598, -0.7369, 0.1218],
[ 0.6759, 0.5139, 0.5207, -0.0887]])
Self Composed Rotation:
[[ 0.3332, 0.3348, -0.8760, 0.0977],
[-0.1811, 0.3484, -0.0382, -0.9189],
[ 0.9253, -0.0448, 0.3112, -0.2123],
[-0.0080, 0.8744, 0.3666, 0.3179]])
📌 The composition of two rotation matrices in SO(4) is generally not commutative.
Inverse
The implementation for the inverse of a rotation matrix on SO(4) group, formula A1 is quite simple.
Let’s validate the implementation of the inverse of the SO(4) rotation.
Output
Rotation
[[ 0.5632, -0.3618, 0.7366, 0.0966],
[ 0.1468, -0.7427, -0.4104, -0.5082],
[ 0.8125, 0.4014, -0.4227, -0.0105],
[ 0.0336, -0.3954, -0.3321, 0.8557]])
Inverse Rotation:
[[ 0.5632, 0.1468, 0.8125, 0.0336],
[-0.3618, -0.7427, 0.4014, -0.3954],
[ 0.7366, -0.4104, -0.4227, -0.3321],
[ 0.0966, -0.5082, -0.0105, 0.8557]])Projection
The method project implements the algorithm [A2] and its 3 steps.
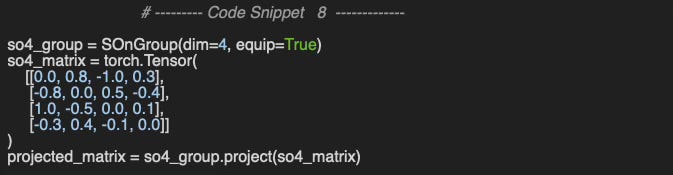
Final let’s evaluate the projection of a given matrix to the SO(4) manifold
Output
Matrix:
0.0000 0.8000 -1.0000 0.3000
-0.8000 0.0000 0.5000 -0.4000
1.0000 -0.5000 0.0000 0.1000
-0.3000 0.4000 -0.1000 0.0000
2025-06-25 16:30:38,766 - INFO -
Projected matrix:
-0.0000 0.4436 -0.8872 -0.1267
-0.4436 0.0000 0.1267 -0.8872
0.8872 -0.1267 0.0000 -0.4436
0.1267 0.8872 0.4436 -0.0000🧠 Key Takeaways
✅ SO(4) has found applications across diverse domains, from equivariant neural networks to protein folding.
✅ Its algebraic structure shares many properties with the more familiar SO(2) and SO(3) groups.
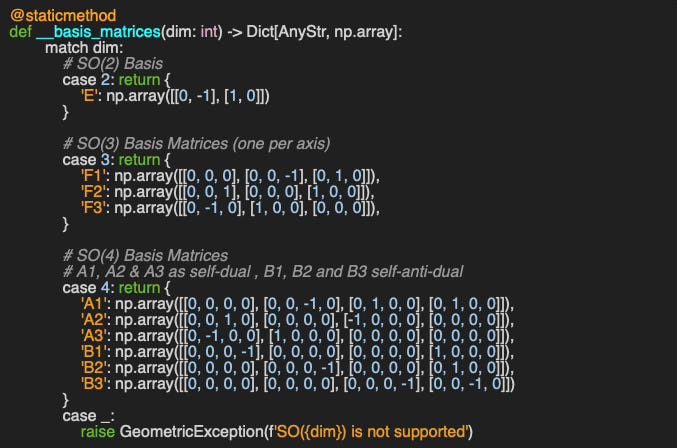
✅ Elements of the SO(4) Lie algebra can be constructed using six basis matrices — three self-dual and three anti-self-dual.
✅ Visualizing elements of the SO(4) group remains a challenge due to its higher dimensionality. This post presents two intuitive approaches:
Decomposing SO(4) rotations into pairs of SO(3) rotation matrices,
Animating the projection of a 4D hypersphere onto 3D space.
📘References
Riemannian Manifolds: Foundational Concepts - Hands-on Geometric Deep learning - 2025 - P. Nicolas
Riemannian Manifolds: Hands-on with Hypersphere Hands-on Geometric Deep learning - 2025 - P. Nicolas
Taming Symmetry: A Dive into Lie groups with Python Hands-on Geometric Deep learning - 2025 - P. Nicolas
so(4) is isomorphic to so(3) + so(3) math.stackexchange
Mastering Special Orthogonal Groups with Practice
geomstats: a Python Package for Riemannian Geometry in Machine Learning N. Miolane, J. Mathe, C. Donnat, M. Jorda, X. Pennec
🛠️ Exercises
Q1: For two elements A and B in the Lie algebra so(4) (represented as 4×4 skew-symmetric matrices), under what condition does the following equality hold?
Q2: Is Rodrigues’s rotation formula applicable to the Lie algebra so(4)?
Q3: What is the purpose of projecting a matrix A onto the manifold SO(4)?
Q4: Can you implement the code to confirm that the composition of two rotation matrices in SO(4) is generally not commutative?
💬 News & Reviews
This section focuses on news and reviews of papers pertaining to geometric deep learning and its related disciplines.
Paper Review: Topological Deep Learning: Going Beyond Graph Data M. Hajij & all - May 2023
Exploring non-Euclidean datasets but finding Graph Neural Networks (GNNs) limiting?
This comprehensive paper offers an excellent introduction to Topological Deep Learning (TDL). It begins with a clear definition of TDL, an extensive glossary, and a detailed discussion of the advantages of using topological structures for modeling heterogeneous data in machine learning.
Through intuitive examples, the authors show how relational and domain-based data can be enriched by augmenting graphs and meshes with higher-order relations—such as cells—capturing more complex structures.
The core focus lies on simplicial, combinatorial, and cell complexes, culminating in hypergraphs as expressive tools for modeling higher-order interactions. These structures provide a natural extension to GNNs, complementing message-passing and pooling operations with geometric symmetries, invariance, and equivariance.
The paper delves into the algebraic and structural foundations of combinatorial complexes, covering homomorphisms, pooling mechanisms, neighborhood operators, and associated matrix representations. It then introduces Combinatorial Complex Neural Networks for rank < 4, illustrating classification and prediction tasks within these structures.
A key contribution is the introduction of a push-forward operator—distinct from the differential geometry concept—which generalizes permutation-invariant aggregation to complex-based learning.
The paper concludes by surveying tools and libraries for TDL, including TopoNetX, and provides datasets to facilitate experimentation in this emerging area of AI.
Appendix
Definition of the basis matrices for so2, so3 and so4 Lie groups, implemented as a private static method.
Patrick Nicolas has over 25 years of experience in software and data engineering, architecture design and end-to-end deployment and support with extensive knowledge in machine learning.
He has been director of data engineering at Aideo Technologies since 2017 and he is the author of "Scala for Machine Learning", Packt Publishing ISBN 978-1-78712-238-3 and Geometric Learning in Python Newsletter on LinkedIn.