SE(3): The Lie Group That Moves the World
After years of feeling daunted by Lie groups and algebras, I finally took the plunge into exploring these fascinating smooth manifolds. This article offers an introduction to the widely-used 3 dimensional Special Euclidean Group, SE(3).
Table of contents
🎯 Why this Matters
Purpose: Due to their mathematical complexity, Lie groups—especially SE(3)—can seem daunting to scientists outside fields like robotics, quantum computing, or computer vision. This article aims to demystify this foundational concept in geometric deep learning.
Audience: Data scientists and engineers looking to expand their toolkit with non-linear modeling and manifold learning techniques.
Value: : How to calculate an element of the 3D Special Euclidean group (SE3) from a given rotation matrix and translation vector in the tangent space, including the implementation of operations for computing the inverse and composition of SE3 group elements.
🎨 Modeling & Design Principles
⚠️ I strongly recommend to review my articles introducing Lie Groups Taming Symmetries: A Dive into Lie groups with Python
Overview
Lie groups—and SE(3) (Special Euclidean group in 3D) in particular—play a foundational role in geometric deep learning, computer vision, robotics, and physics-informed machine learning. Lie groups model symmetries in data and domains. Machine learning models that respect or exploit these symmetries are more data-efficient and generalize better.
The most common applications in machine learning are:
Equivariant Neural Networks: Molecular modeling (e.g., SE(3)-Transformer [ref 2]), 3D object recognition, point cloud analysis and Protein structure prediction.
3D Computer Vision and Robotics: Pose estimation, Visual Simultaneous Localization and Mapping and Trajectory prediction and planning.
Physics-Informed ML & Simulation: Particle dynamics, Rigid body simulations and Quantum interactions
Manifold Learning: invariant features, dimension reduction
⚠️ Disclaimer : A thorough tutorial and explanation of Lie groups, Lie algebras, and geometric priors for deep learning models is beyond the scope of this article. Instead, the following sections concentrate on experiments involving key elements and operations on Lie groups using the Geomstats Python library [ref 3, 4].
Smooth Manifolds & Lie Groups
A smooth manifold is a topological space that locally resembles Euclidean space and allows for smooth (infinitely differentiable) transitions between local coordinate systems. This structure allows for the use of calculus on the manifold [ref 5].
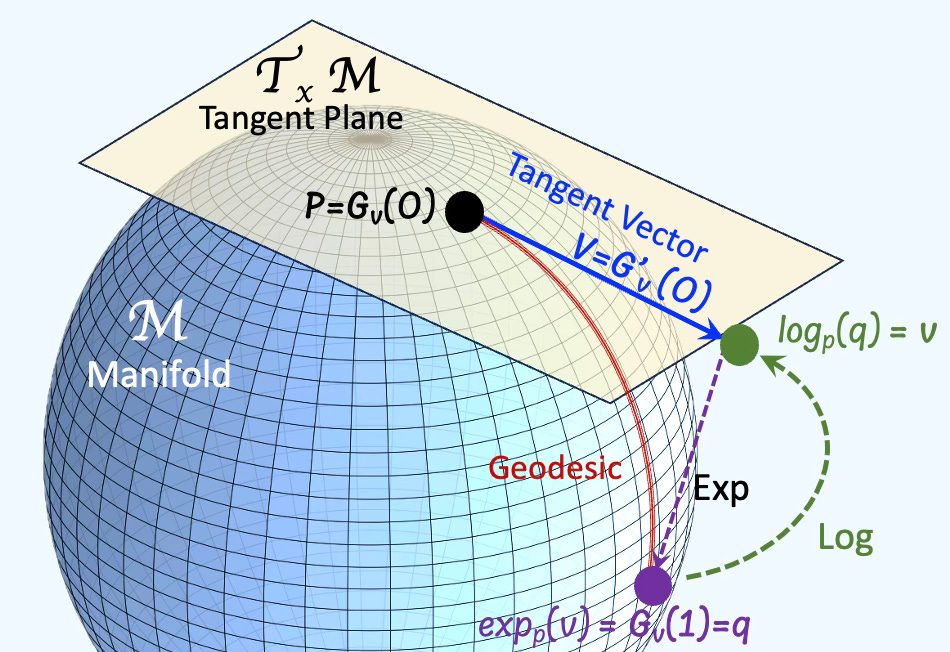
The tangent space at a point on a manifold is the set of tangent vectors at that point, like a line tangent to a circle or a plane tangent to a surface.
Tangent vectors can act as directional derivatives, where you can apply specific formulas to characterize these derivatives.
Fig. 1 Spherical manifold with tangent plane and exponential Exp logarithm Log maps
⚠️. Lie groups do not resemble spheres or hyperspheres, but we use them here purely for illustrative purposes.
In differential geometry, a Lie group is a mathematical structure that combines the properties of both a group and a smooth manifold. It allows for the application of both algebraic and geometric techniques. As a group, it has an operation (like multiplication) that satisfies certain axioms (closure, associativity, identity, and invertibility) [ref 6, 7].
From a mathematical perspective, a Lie group must support
with the following condition.
inversion of a smooth map is smooth maps
multiplication (a.k.a. product or composition) of two smooth maps is a smooth maps
Special Euclidean Group SE(3)
The Euclidean group is a subset of the broader affine transformation group. It contains the translational and orthogonal groups as subgroups [ref 8]. Any element of SE(n) can be represented as a combination of a translation and an orthogonal transformation, where the translation b can either precede or follow the orthogonal transformation A,
The 3-dimension Special Euclidean group (SE3) is described as a 4x4 matrix with R, 3 x 3 rotation matrix and t a 3 dimension vector (eq 1]
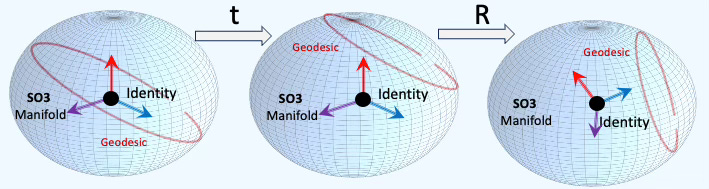
Fig. 2 Visualization of SE3 group using a Hypersphere for translation and rotations
The tangent vector is defined as a 4 x 4 matrix algebra
The relationship between the rotation matrix R and the omega is given by
Geomstats
Geomstats is a free, open-source Python library designed for conducting machine learning on data situated on nonlinear manifolds, an area known as Geometric Learning. This library offers object-oriented, thoroughly unit-tested features for fundamental manifolds, operations, and learning algorithms, compatible with various execution environments, including NumPy, PyTorch, and TensorFlow.
The library is structured into two principal components:
geometry: This part provides an object-oriented framework for crucial concepts in differential geometry, such as exponential and logarithm maps, parallel transport, tangent vectors, geodesics, and Riemannian metrics.
learning: This section includes statistics and machine learning algorithm
⚙️ Hands-on with Python
This article emphasizes the practical applications of Lie theory in the case of SE(3) manifold.
Environment
Libraries: Python 3.12, Geomstats 2.8.0
Source code is available at GitHub.com/patnicolas/geometriclearning/Lie
To enhance the readability of the algorithm implementations, we have omitted non-essential code elements like error checking, comments, exceptions, validation of class and method arguments, scoping qualifiers, and import statements.
Setup
First, we define the basic SE3 group element as the data class SE3Element. It has three components.
group_element: Element of SE3 group
algebra_element: 4x 4 matrix representation with 3x3 rotation and 1x3 translation
descriptor: Optional descriptor for debugging purpose.
Example of SE3 element:
- SE3 Algebra:
[[ 1. 0. 0. 1.]
[ 0. 0. -1. 3.]
[ 0. 1. 0. 2.]
[ 0. 0. 0. 1.]]
- SE3 Group:
[[ 2.718 -0. 0. 2.718]
[ 0. 0.54 -0.841 3.193]
[ 0. 0.841 0.54 5.024]
[ 0. -0. 0. 2.718]]A 4x4 Lie algebra element can be generated from unit element (3 rotation and 3 translation).
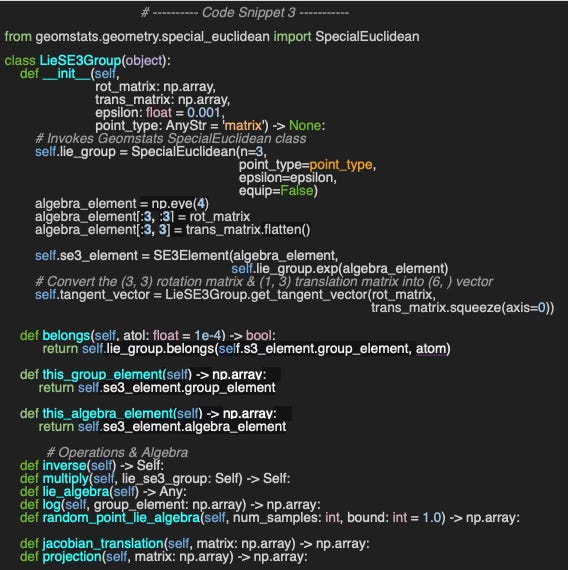
We adopt the same object-oriented approach as used with the Special Orthogonal Group to describe the components and operations on the SE(3) manifold. The LieSE3Group class encapsulates the definition of the Special Euclidean group and its associated operations.
A SE3 group is fully defined by
the SpecialEuclidean (dim = 3), lie_group
An SE3 element, se3_element composed of 4x 4 algebra and group elements
The default constructor, __init__ creates a new element in the SE3 manifold, se3_element, using the Lie Algebra created from 3x3 rotation matrix rot_matrix and 1x3 translation matrix trans_matrix, error tolerance, epsilon for point on the manifold, and point_type for the representation for points (matrix or vector).
The method belongs invokes the Geomstats method of the same name, and will be applied to validate the Lie group properties for inversion and multiplication
Although the LieSE3Group class includes numerous operations, this article focuses on the implementation of two fundamental Lie group properties: inversion and multiplication.
📌 Dual representation As previously noted, a Lie group embodies both a group structure and a smooth manifold. This dual nature is captured by the point_type, parameter: ‘matrix’ represents the group structure, while ‘vector’ corresponds to the manifold representation.
The initialization of the algebra_element and se3_element in the constructor is illustrated below:
Fig. 3 Illustration of the generation of Lie algebra and Group elements from rotation and translation in LieSE3Group class constructor
The equations 2 and 3 are implemented by the method get_tangent_vector as follows:
This method is used to generate the 6-element representation of the SE(3) algebra element from the 3 x 3 rotation matrix, and 1 x 3 translation matrix. The algebra element is created as part of the constructor.
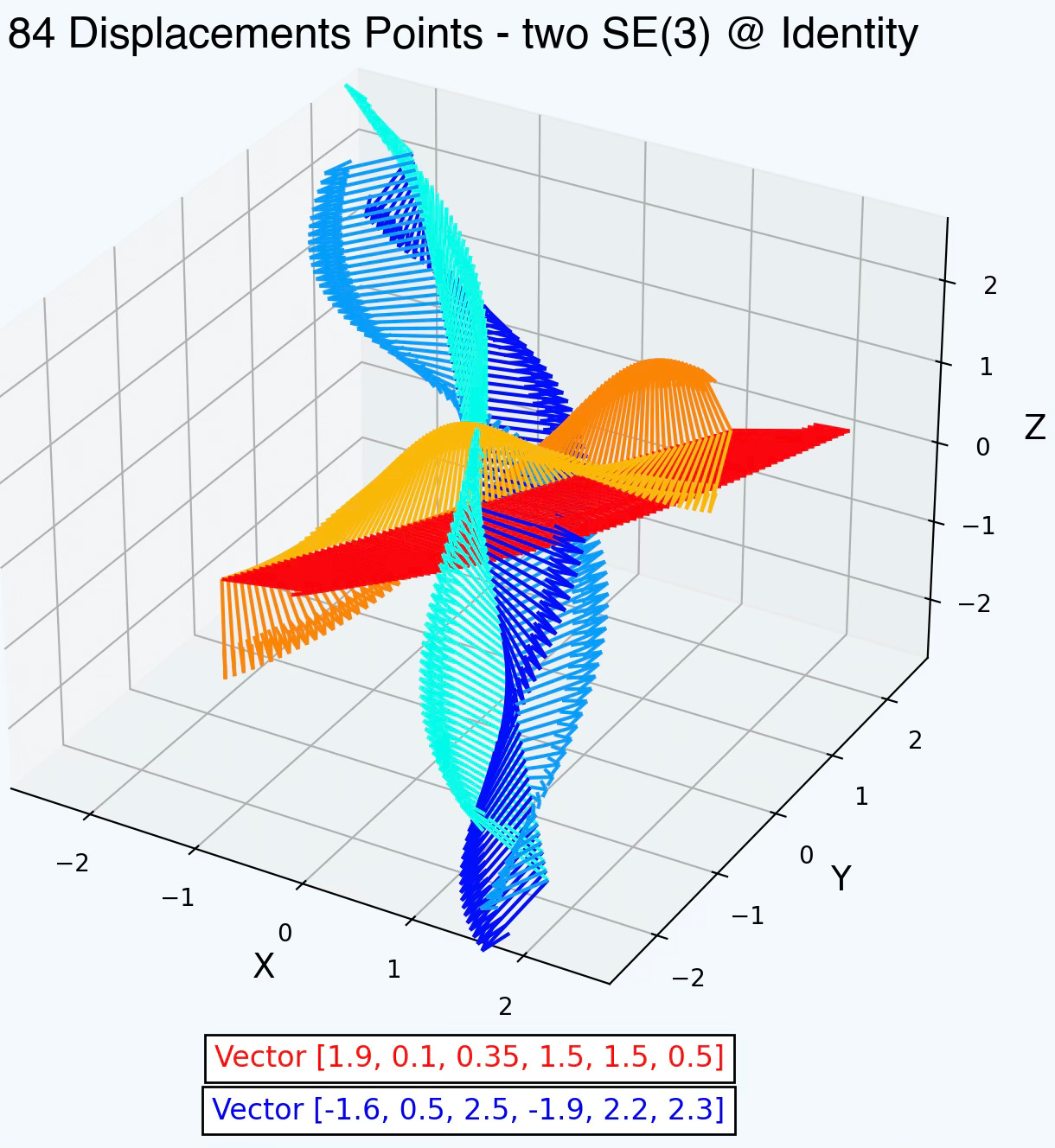
📈 Visualization Displacements
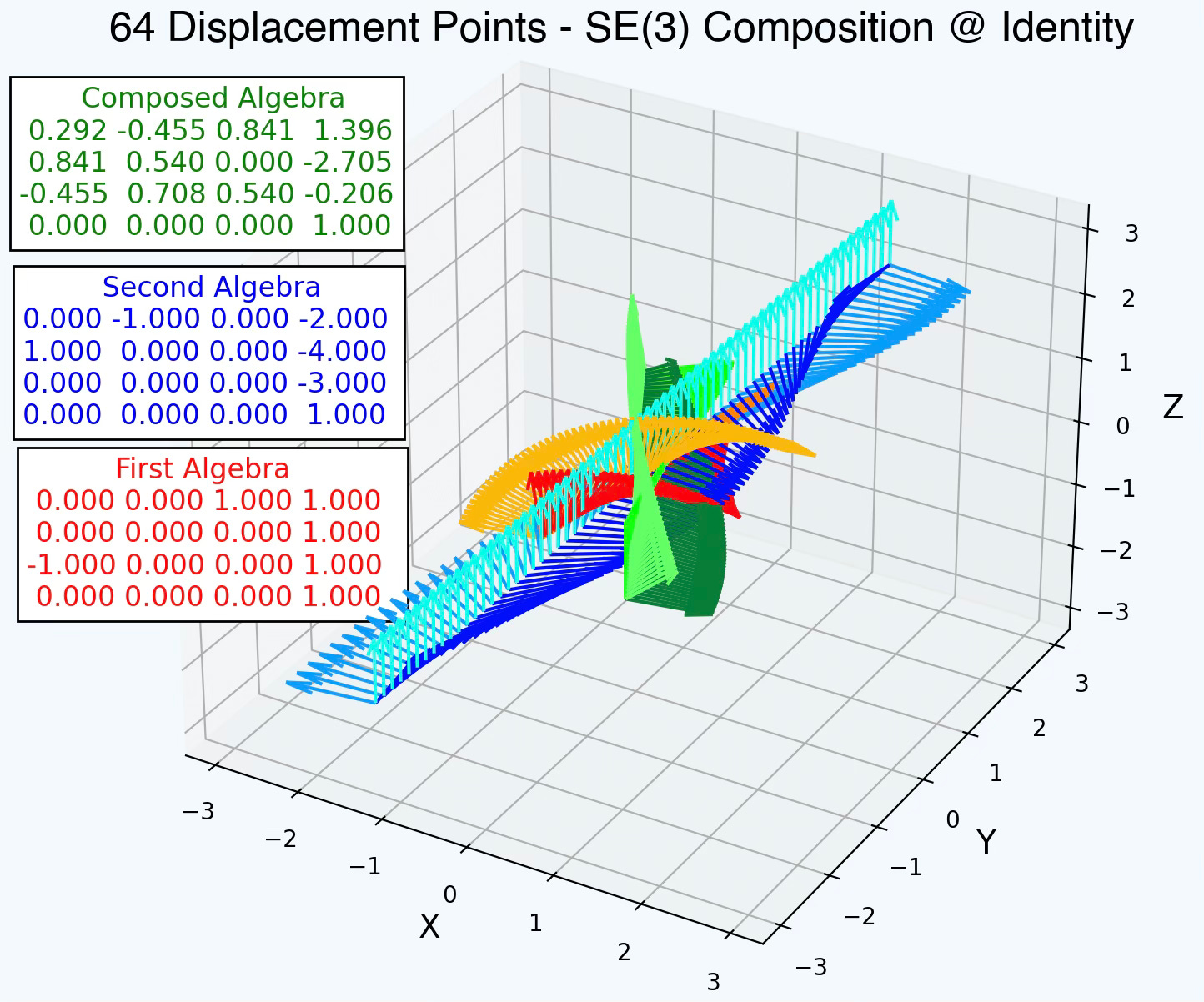
The first step is to represent or simulate the rotation and translation of SE(3) along a path known as displacements. The following plot illustrates the morphism during displacement of two SE3 element with rotation along 3 axes with different color.
Fig. 4 Illustration of two SE(3) group with 84 displacement points
Visualizing SE(3) elements falls outside the scope of this article and requires a minor modification to the Trihedron.draw method's signature and implementation, as detailed in the appendix.
The visualization is implemented in a subclass of LieSE3Group, SE3Visualization. The description of the visualization is beyond the scope of this article. However, the code is available on GitHub [ref 9].
Inversion
Inversion is a fundamental algebraic operation in any Lie group, and SE(3) is no exception. It is implemented through the inverse method, which internally leverages Geomstats' built-in inversion functionality.
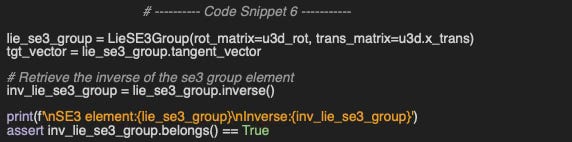
Let’s compute the inverse of an SE(3) element defined by a rotation about the y-axis (y_rot) and a translation along the x-axis (x_trans).
Output:
SE3 element:
SE3 group element:
0.540 0.000 0.841 1.510
0.000 1.000 0.000 0.000
-0.841 0.000 0.540 -0.668
0.000 0.000 0.000 2.718
SE3 Algebra
0.000 0.000 1.000 1.000
0.000 0.000 0.000 0.000
-1.000 0.000 0.000 0.000
0.000 0.000 0.000 1.000
Inverse:
SE3 group element:
1.144 0.000 -1.280 -1.971
0.000 2.718 0.000 0.000
1.280 0.000 1.144 -2.885
0.000 0.000 0.000 2.718
SE3 Algebra
0.540 0.000 -0.841 -1.378
0.000 1.000 0.000 -0.000
0.841 0.000 0.540 -0.909
0.000 0.000 0.000 1.000The assertion succeeds to validate the insertion property that the inverse of a Lie group is also a Lie group.
⚠️ We use matrix (default) as point type representation because we are dealing with algebraic expressions (Lie algebra).
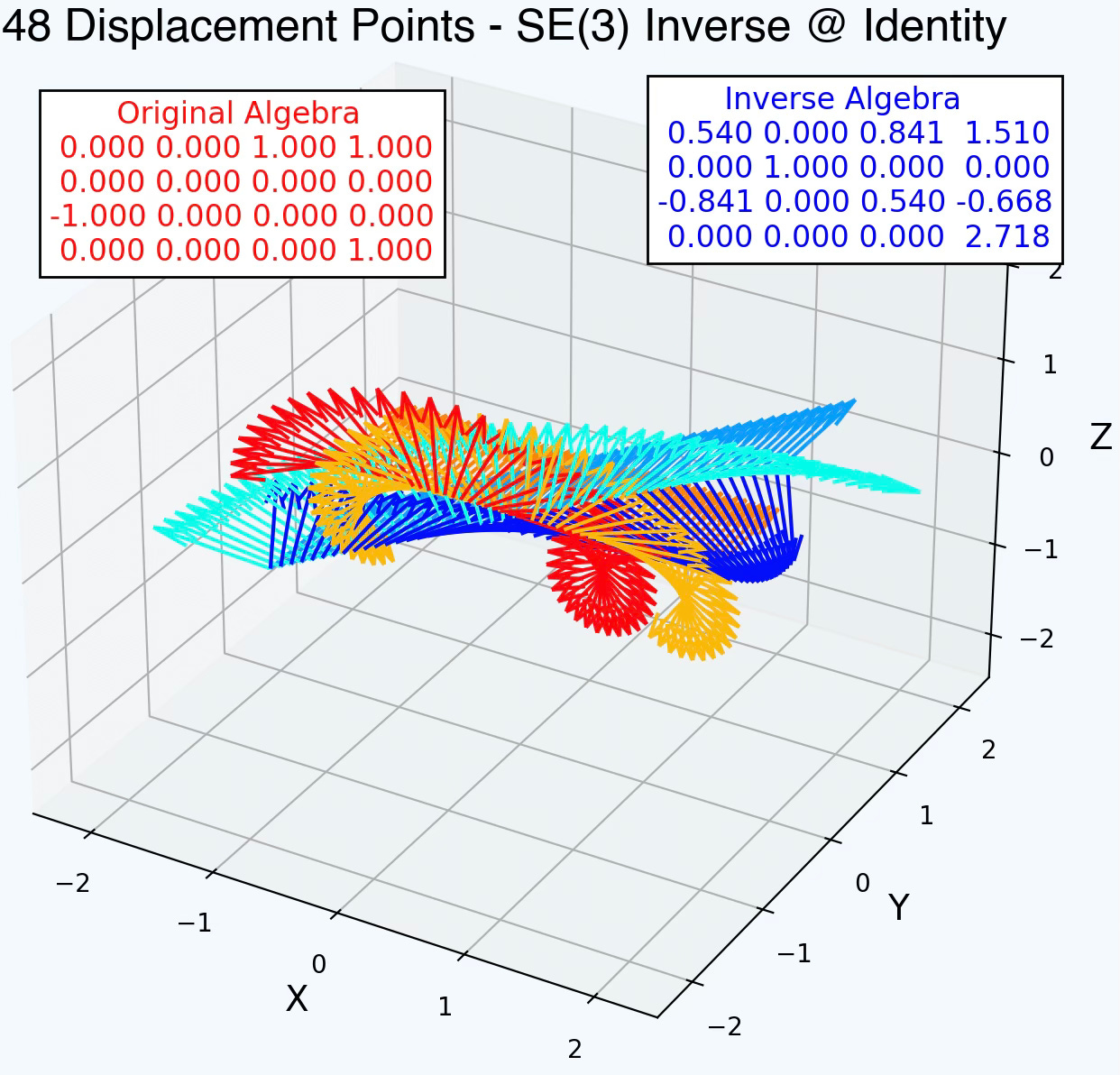
Let’s visualize the original and inverse SE3 elements using 48 points.
Fig. 5 Visualization of Lie algebra for inverse of SE(3) element with 48 displacement points
Multiplication
We implement the multiplication (also known as composition) of two SE(3) elements in the multiply method (code snippet 7), which internally calls Geomstats' compose function. The resulting Lie group inverse is then constructed by extracting the 3×3 rotation matrix and 1×3 translation vector from the composed matrix, composed_group_point.
📌 Multiplication or Composition? Many Lie group implementations, including Geomstats, refer to the group multiplication operation as "compose." However, we have chosen to retain the original terminology: "multiply."
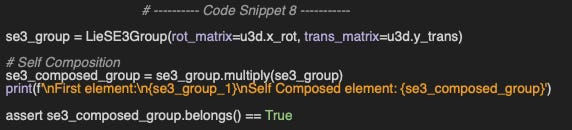
Self composition
The first test consists of composing a SE3 group element with itself as described in code snippet 8.
Output:
SE3 element:
SE3 group element:
1.000 0.000 0.000 0.000
0.000 0.540 -0.841 1.510
0.000 0.841 0.540 0.668
0.000 0.000 0.000 2.718
SE3 Algebra
0.000 0.000 0.000 0.000
0.000 0.000 -1.000 1.000
0.000 1.000 0.000 0.000
0.000 0.000 0.000 1.000
Self Composed element:
SE3 group element:
2.718 0.000 0.000 0.000
0.000 0.405 -0.520 4.104
0.000 0.520 0.405 6.666
0.000 -0.000 -0.000 2.718
SE3 Algebra
1.000 0.000 0.000 0.000
0.000 -0.416 -0.909 4.357
0.000 0.909 -0.416 3.448
0.000 0.000 0.000 1.000The successful assertion validates the composition property of Lie groups.
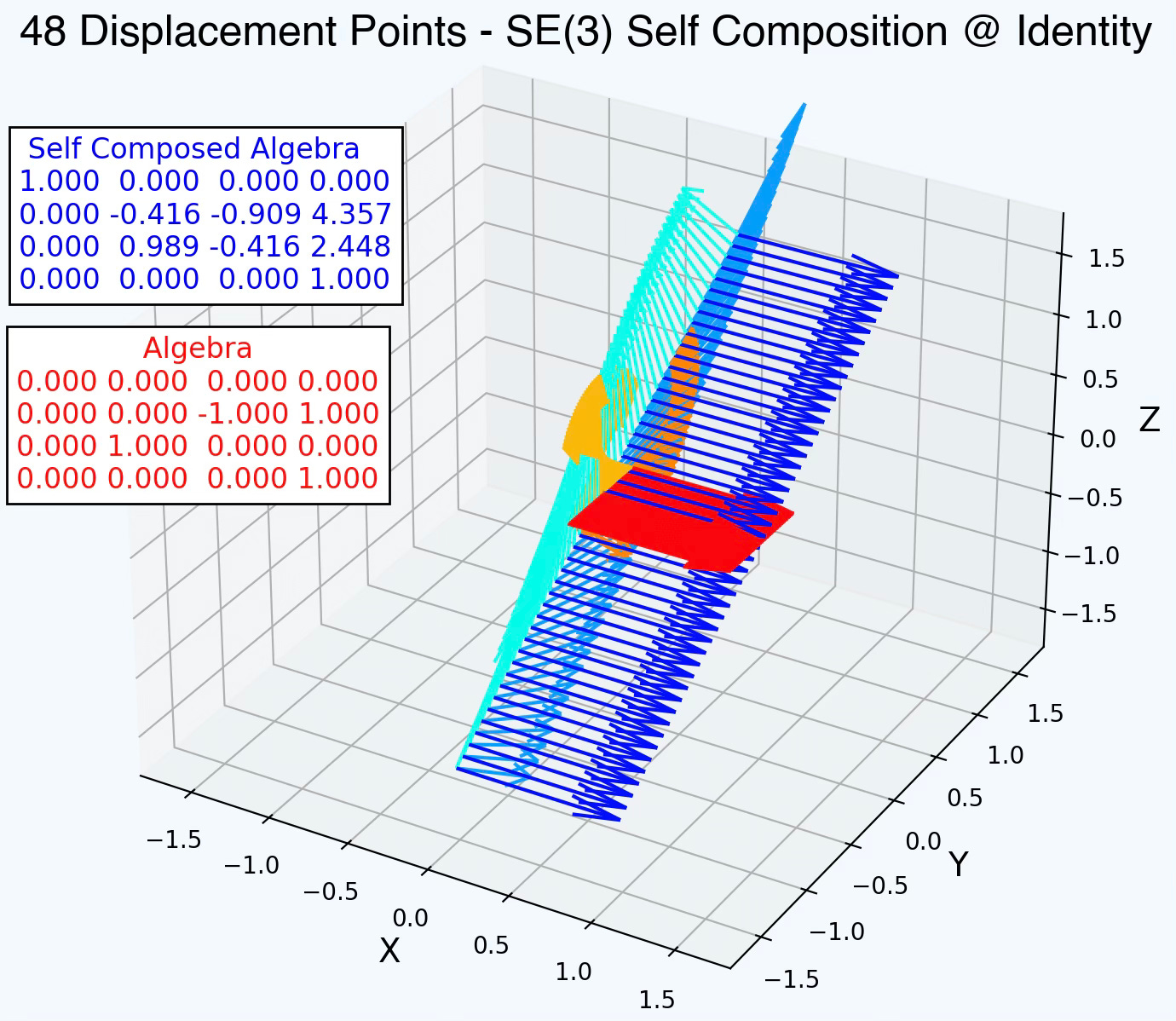
Let’s visualize the original and inverse SE3 elements using 24 points
Fig. 6 Visualization of Lie algebra for self composition of a SE(3) element with 48 displacement points
The last test consists of validating the multiplication property with two different SE3 elements.
Output:
First element:
SE3 group element:
0.540 0.000 0.841 2.178
0.000 1.000 0.000 1.718
-0.841 0.000 0.540 0.841
0.000 0.000 0.000 2.718
SE3 Algebra
0.000 0.000 1.000 1.000
0.000 0.000 0.000 1.000
-1.000 0.000 0.000 1.000
0.000 0.000 0.000 1.000
Second element
SE3 group element:
0.540 -0.841 0.000 -0.346
0.841 0.540 -0.000 -7.375
-0.000 -0.000 1.000 -5.155
0.000 0.000 0.000 2.718
SE3 Algebra
0.000 -1.000 0.000 -2.000
1.000 0.000 0.000 -4.000
0.000 0.000 0.000 -3.000
0.000 0.000 0.000 1.000
Composed element:
SE3 group element:
0.935 -0.174 1.148 2.932
1.148 1.560 0.531 -4.693
-0.174 1.253 1.560 -2.749
0.000 0.000 0.000 2.718
SE3 Algebra
0.292 -0.455 0.841 1.396
0.841 0.540 0.000 -2.705
-0.455 0.708 0.540 -0.206
0.000 0.000 0.000 1.000Finally, we visualize the composition of the 4 x 4 SE3 elements with 36 points.
Fig. 7 Visualization of Lie algebra for composition of SE(3) elements with 64 displacement points
🧠 Key Takeaways
✅ The Special Euclidean Group SE(3) is a foundational Lie group widely used in Equivariant Neural Networks, robotics, 3D computer vision, physics-based simulations, motion planning, Physics-Informed Machine Learning, and manifold learning.
✅ Geomstats equips data scientists and engineers with a comprehensive toolkit to design, experiment with, and apply SE(3)-based models.
✅ SE(3) elements, when represented with point_type='matrix', take the form of 4×4 transformation matrices composed of a 3×3 rotation matrix and a 3D translation vector.
✅ Any SE(3) transformation can be constructed from a linear combination of three unit rotations (one per axis) and three unit translations.
✅ The behavior of SE(3) transformations can be intuitively visualized using displacement points with point_type='vector'.
📘 References
SE(3) Transformers: 3D Roto-Translation Equivariant Attention Networks - F. Fuch, D. Worrall, V. Fisher, M. Welling
Explore Geometric Learning with Geomstats P. Nicolas - Substack
Introduction to Differential Geometry - J. Robbin, D. Salamon - ETH Zurich
Basics of Classical Lie groups: The Exponential Map, Lie Groups, and Lie Algebras University of Pennsylvania
Introduction to Lie Groups and Lie Algebras - A. Kirillov Jr. SUNY as Stony Brook
The Lie group SE(3) - University of Pennsylvania
🛠️ Exercises
Q1: What are the two point types used in SE(3)?
Q2: The exponential map generates SE(3) elements from a 4×4 Lie algebra matrix. How can we compute the corresponding Lie algebra matrix from a given SE(3) element?
Q3: Can you provide Python code, using numpy to construct a 4×4 SE(3) matrix from a given 3×3 spatial rotation matrix and a 3D translation vector?
Q4: Additionally, can you provide code to verify SE(3) multiplication is not commutative?
Q5: What is the condition on SE(3) group element for the tangent space to be a Lie Algebra?
👉 Answers
Appendix
💬 News & Reviews
This section focuses on news and reviews of papers pertaining to geometric deep learning and its related disciplines.
Paper review: Riemannian Score-Based Generative Modelling V. De Bortoli, E Mathieu, M. Hutchinson, J. Thornton, Y. Whye Teh, A. Doucet
Diffusion models, or score-based generative models, progressively add noise to create a generative model that reverses the noise addition process over time. Although effective, these models primarily utilize data in Euclidean space and often fail to capture the intrinsic geometry of complex data such as proteins, geological formations, or high-energy physics components.
This paper outlines four steps to adapt diffusion models to manifolds:
Modify the noise addition process to suit manifolds using the Riemannian gradient.
Incorporate Brownian motion into the Euclidean time-reversal formula.
Implement Geodesic random walks to approximate sampling from stochastic differential equations.
Approximate and evaluate the drift in the time-reversal process.
The authors provide well-documented pseudocode for the geodesic random walk and the training/sampling methodology for the Riemannian Score-Based Generative model. The evaluation of this model, using datasets related to earth and climate science on a hypersphere, and synthetic datasets for SO(3), demonstrates a significant improvement in the log-likelihood score.
Code is available on Github
Patrick Nicolas has over 25 years of experience in software and data engineering, architecture design and end-to-end deployment and support with extensive knowledge in machine learning.
He has been director of data engineering at Aideo Technologies since 2017 and he is the author of "Scala for Machine Learning", Packt Publishing ISBN 978-1-78712-238-3 and Geometric Learning in Python Newsletter on LinkedIn.