Mastering Special Orthogonal Groups With Practice
Lie Special Orthogonal Groups SO(n) are essential in machine learning when dealing with rotational symmetries, enabling models to be more robust, data-efficient, and physically accurate. They provide a mathematical framework to encode geometry directly into neural architectures.
Table of Contents
🎯 Why this matters
Purpose: Lie groups SO(2) and SO(3) play a fundamental role in machine learning, particularly in geometric deep learning, computer vision, robotics, and molecular modeling.
Audience: Data scientists and engineers intrigued by Geometric Deep Learning or involved in encoding geometric priors to models for computer vision, molecular simulation or robotics.
Value: Learn how to implement the Lie algebra and operations for Special Orthogonal Groups.
🎨 Modeling & Design Principles
⚠️ A thorough tutorial and explanation of Lie groups, Lie algebras, and geometric priors for deep learning models is beyond the scope of this article. Instead, the following sections concentrate on experiments involving key elements and operations on Lie groups using the Geomstats Python library.
Overview
📌 Smooth manifolds and Lie groups have been introduced and put in practice in previous articles of this newsletter [ref 1, 2 & 3]
Differential Geometry
Here is a brief re-introduction to some basic concepts:
A manifold is a topological space that, around any given point, closely resembles Euclidean space.
A smooth (or differential) manifold is a topological space that locally resembles Euclidean space and allows for smooth (infinitely differentiable) transitions between local coordinate systems. This structure allows for the use of calculus on the manifold.
A Riemannian manifold is a smooth manifold that comes with a metric tensor, providing a way to measure distances and angles.
The tangent space at a point on a manifold is the set of tangent vectors at that point, like a line tangent to a circle or a plane tangent to a surface.
Tangent vectors can act as directional derivatives, where you can apply specific formulas to characterize these derivatives.
A geodesic is the shortest path (arc) between two points in a Riemannian manifold.
In differential geometry, a Lie group is a mathematical structure that combines the properties of both a group and a smooth manifold. Lie groups play a crucial role in Geometric Deep Learning by modeling symmetries such as rotation, translation, and scaling.
Special Orthogonal Groups
The Special Orthogonal n-dimensional Groups SO(n) are the Lie groups that represents rotations in n-dimensional space. It is widely used in robotics, physics, computer vision, and geometric deep learning to describe rigid body rotations without scaling or reflection.
[1] Enforces orthogonally for which the unit of rotations are mutually perpendicular. It is equivalent to O(n) group.
[2] Ensures rotation and preserves orientation.
The dimension of a SO(n) group is computed as
Example: SO(3) has 3 dimensions, SO(4) has 6 dimensions and SO(5) has 10 dimensions
Special Orthogonal Lie groups have many applications:
Rotational Symmetries: As many physical and visual systems are invariant or equivariant to rotations, these symmetries allows models to reduce redundancy and improve generalization
Equivariant Neural Networks: Equivariant and tensor field networks uses SO(3) for tasks such s 3D shapes, Molecular modeling and simulations.
Data Augmentation: Rotations are used to augment training data imposing rotation-invariant constraints during training.
Visualization
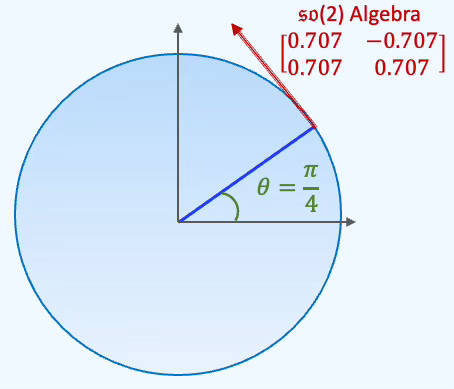
The visualization of Lie groups and algebras, even in 2 and 3 dimensional space is arduous. Here is an illustration of 2D rotation matrices (for angle displacement 45 degree).
Fig. 1 Illustration of SO(2) rotation group with its algebra
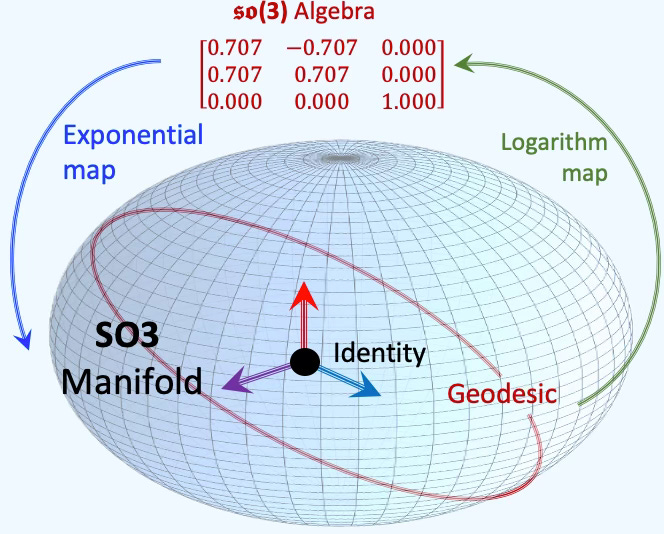
Similarily, the following graph visualizes a 3 dimensional rotation matrix and the action on the SO(3) group.
Fig. 2 Illustration of SO(3) rotation group with its algebra
⚠️ Lie groups do not resemble spheres or hyperspheres, but we use them here purely for illustrative purposes.
Exponential & Logarithm Maps
Given a Riemannian manifold M and a tangent space TM, an exponential map is a map from a subset of a tangent space of a Riemannian manifold. Given a tangent vector v at a point p on a manifold, there is a unique geodesic Gv that satisfy Gv(0)=pand G’v(0)=v. The exponential map is defined as expp(v)= Gv(1).
In the case of SO(n) group, the exponential map is defined as
For the same Riemannian manifold, given a geodesic Gv starting at point p with a direction v, the logarithm map is defined as
In the case of n-dimensional rotation group, SO(3) the logarithm map can be expressed as
The following graphic illustrates the relation between SO(3) group and its algebra and the relation between exponential and logarithm maps.
Fig. 3 Illustration of Exponential and Logarithm maps
The so3 Algebra is the tangent space at identity.
⚠️ The exponential map exp: so(3)→SO(3) is not injective. For example, A being a rotation matrix, exp(A) = exp(A+2πv). Consequently, multiple algebra elements (or matrices) map to the same group (rotation). So the validation of exponential and logarithm maps for any algebra A, log(exp(A)) = A requires A in [−π,π].
Rodrigues’s Formula
In Lie algebra so(3), a skew-symmetric matrix is a rotation around a single axis in 3D, making so(3) isomorphic to RxRxR. Therefore, it is possible to compute a close-form expression for the exponential map.
Rodrigues’s formula is a closed-form expression for the exponential of a skew-symmetric matrix A on SO3 Algebra associated with a vector v
Inverse & Composition
The inverse of a rotation matrix SO(n) is equal to its transpose.
The composition of SO(n) refers to the successive application of rotations represented by these matrices (a.k.a. matrix multiplication). This composition is also associative, meaning the way you group the multiplications doesn't change the result although the order of operations matters (right-to-left).
For two groups f, g and two n-dimensional matrices F, G on the Lie Algebra
Projection
The projection of a matrix onto SO(n) refers to finding the closest matrix R in SO(n) to a given n x n matrix of real values M, typically one that is not exactly a valid rotation matrix due to noise or numerical errors.
The problem is solved using the Singular Value Decomposition of the input matrix M
The first equations is a classic Singular Value Decomposition. The second equation ensure that orientation (det(A) = +1).
Although the theoretical section applies to Lie Rotation Groups of any dimension, the following implementation focuses of SO(2) and SO(3) groups and associated algebras.
⚠️ While the theoretical discussion is valid for Lie rotation groups in any dimension, the implementation that follows specifically targets the SO(2) and SO(3) groups along with their corresponding algebras. The evaluation of SO(4) is the subject of a future article.
Geomstats
Geomstats is a free, open-source Python library designed for conducting machine learning on data lying on nonlinear manifolds, an area known as Geometric Learning.
The core concept of Geomstats is to incorporate differential geometry principles, such as manifolds and Lie groups, into the development of statistical and machine learning models. This open-source, object-oriented library follows Scikit-Learn’s API conventions for seamless integration [ref 7, 8].
Geomstats serves as a practical tool for gaining hands-on experience with geometric learning fundamentals while also supporting future research in the field.
The Geomstats library is described in detail in the following article Exploring Geometric Learning with Geomstats of this newsletter.
⚙️ Hands‑on with Python
Environment
Libraries: Python 3.12.5, PyTorch 2.5.0, Numpy 2.2.0, Geomstats 2.8.0
Source code is available at Github/PatNicolas/GeometricLearning/Lie/SOnGroup
To enhance the readability of the algorithm implementations, we have omitted non-essential code elements like error checking, comments, exceptions, validation of class and method arguments, scoping qualifiers, and import statements.
Setup
📌 Many articles in this newsletter make use of PyTorch and PyTorch Geometric, so we adopt torch.Tensor as the primary type for representing elements of Lie groups and Lie algebras.
Let's start by encapsulating the functionality of the SO(n) group in a class called SOnGroup. The constructor accepts three parameters:
dim: The dimension of the manifold (e.g., dim=3 for the SO(3) group)
equip: A boolean flag indicating whether the group is equipped with a Riemannian metric (True) or not (False)
atol: The numerical tolerance used when evaluating results
This article focuses on SO(n) as a Lie group not a manifold. Therefore we use ‘matrix’ as the type of representation.
📌 Dual representation As previously noted, a Lie group embodies both a group structure and a smooth manifold. This dual nature is captured in Geomstats by the point_type, parameter: ‘matrix’ represents the group structure, while ‘vector’ corresponds to the manifold representation.
SO(n) Generation & Validation
We need to make sure that any point or matrix is orthogonal [Condition 1] and preserve orientation [Condition 2].
The method belongs of class SOnGroup invokes validate_points.
There are three main approaches to generating random elements of SO(n):
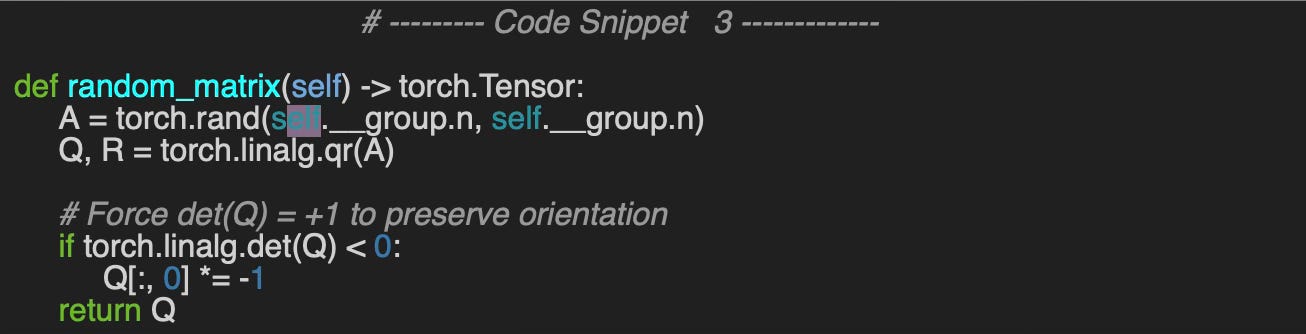
QR decomposition (custom implementation)
Rotation angle normalization, as used in Geomstats
Direct instantiation of rotation matrices from angles
Linear combination of basis rotation matrices.
Let's explore both methods in detail.
The method random_matrix implements the QR decomposition using torch linear algebra module as follows:
The second method is available through the Geomstats library method, SpecialOrthogonal.random_uniform (Code snippet 4).
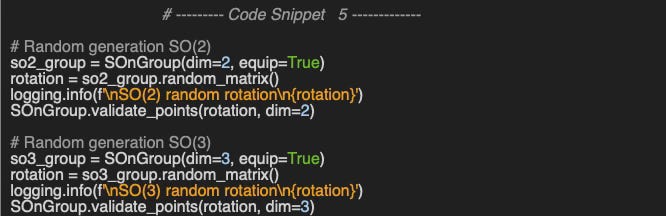
Let’s illustrate this mechanism to generate SO(2) and SO(3) elements (Code snippet 5).
Output:
SO(2) random rotation
[[ 0.6755, -0.7374],
[ 0.7374, 0.6755]]
SO(3) random rotation
[[-0.1969, 0.1159, -0.9736],
[-0.9733, -0.1426, 0.1798],
[-0.1180, 0.9830, 0.1409]]The third method is a strict implementation of the rotation matrices as illustrated in the following code snippet.
The last method consists of combining basic matrices for so2, so3 and so4 to generate rotation matrices. For example a so3 metric can be computed with 3 basis matrices
The basis matrices are defined in the method __basis_matrices described in the Appendix. The generation of rotation matrices through basis matrices is implemented by method, generate_rotation (Code snippet 7).
Exp & Log
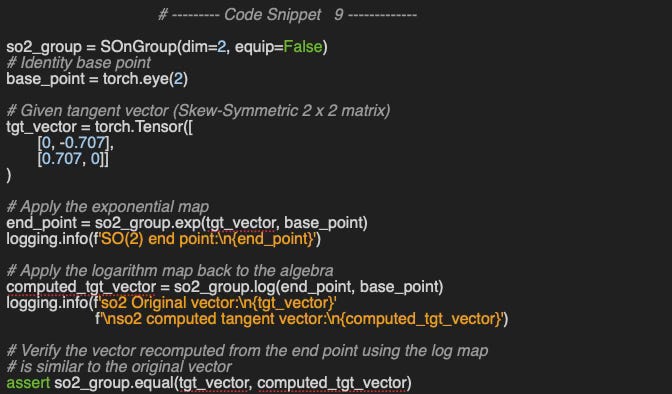
The two methods, exp and log are wrappers around the relevant Geomstats implementations. We just add a validation of input and output tensors (Code snippet 8).
The objective of the following test is to validate both exponential and logarithm maps simultaneously for so2 and so3 algebras.
Output:
SO(2) end point:
tensor([[ 0.7603, -0.6496],
[ 0.6496, 0.7603]])
so2 algebra A:
tensor([[ 0.0000, -0.7070],
[ 0.7070, 0.0000]])
so2 computed algebra log(exp(A)):
tensor([[ 1.4567e-07, -7.0700e-01],
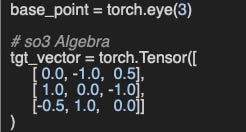
[ 7.0700e-01, 1.2270e-07]])We execute the same validation for a 3 dimensional rotation matrix:
Output:
SO(3) end point:
tensor([[ 0.4837, -0.4585, 0.7455],
[ 0.8715, 0.1740, -0.4585],
[ 0.0805, 0.8715, 0.4837]])
so3 algebra A:
tensor([[ 0.0000, -1.0000, 0.5000],
[ 1.0000, 0.0000, -1.0000],
[-0.5000, 1.0000, 0.0000]])
so3 computed algebra log(exp(A)):
tensor([[-4.0221e-08, -1.0000e+00, 5.0000e-01],
[ 1.0000e+00, 2.7180e-08, -1.0000e+00],
[-5.0000e-01, 1.0000e+00, -1.0216e-07]])The computed algebra log(exp(A)) is equal to the original matrix A within the error tolerance.
Operations
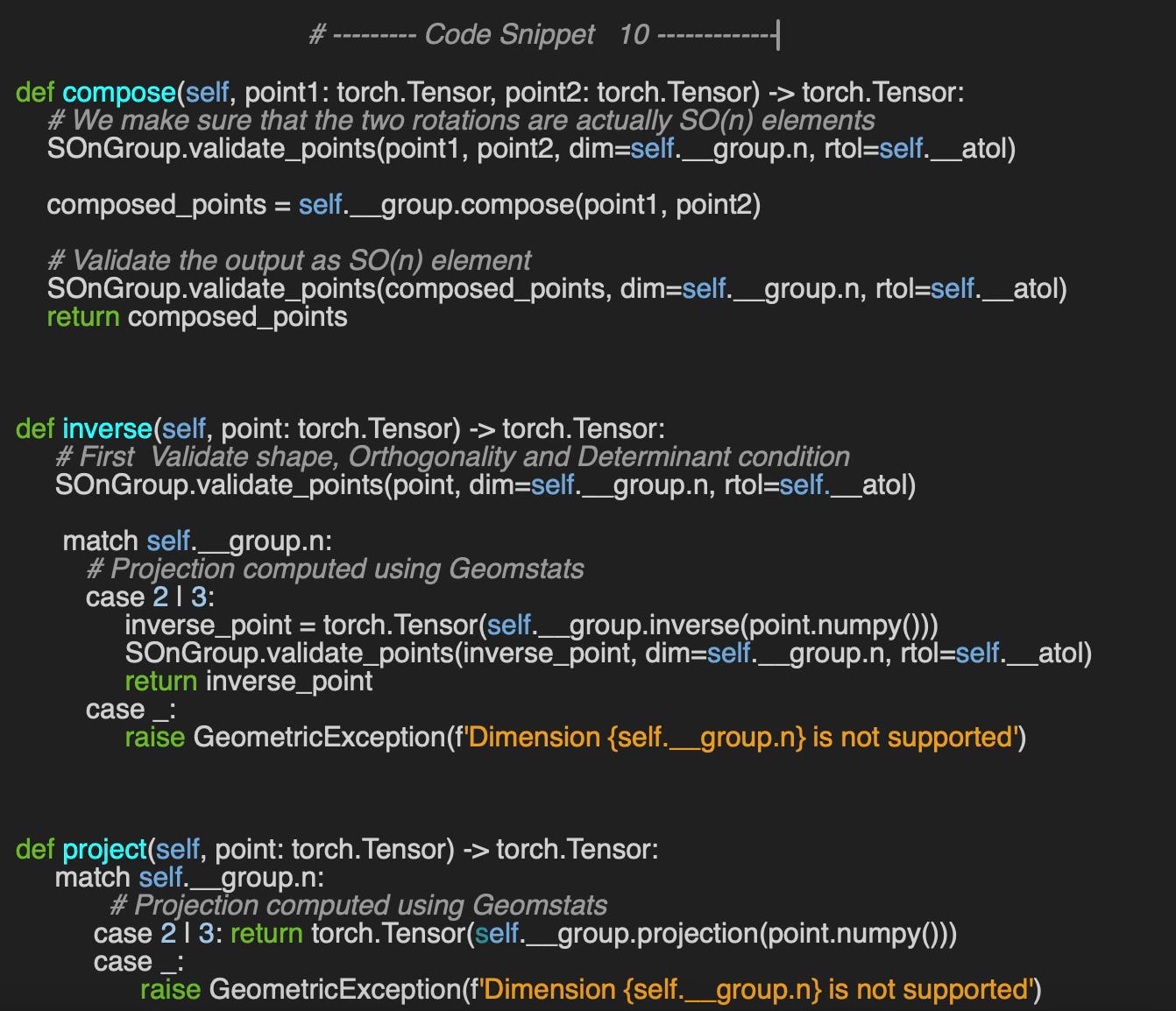
This article highlights three key operations:
compose: combining two SO(n) elements
inverse: computing the inverse of a SO(n) element,
project: Attempt to map an arbitrary n x n matrix to the closest SO(n) element for n = 2, 3
Each method implementation primarily involves validating SO(n) input data, then delegating to the corresponding functions provided by the Geomstats library. We use the differential geometry term, point on the manifold to specify the rotation on SO(n) with n =2 or 3.
Let’s exercise these 3 operations in the context of SO(2) and SO(3) groups.
Example 1: Composition on SO(3)
We evaluate the composition with two scenarios:
Two matrices; 45 and 0 degree angles
Two identical matrices
Output:
Rotation 1:
tensor([[ 0.7071, -0.7071, 0.0000],
[ 0.7071, 0.7071, 0.0000],
[ 0.0000, 0.0000, 1.0000]])
Rotation 2:
tensor([[1., -0., 0.],
[0., 1., 0.],
[0., 0., 1.]])
Composed rotation:
tensor([[ 0.7071, -0.7071, 0.0000],
[ 0.7071, 0.7071, 0.0000],
[ 0.0000, 0.0000, 1.0000]])
Self composed rotation:
tensor([[-1.2688e-08, -1.0000e+00, 0.0000e+00],
[ 1.0000e+00, 1.2688e-08, 0.0000e+00],
[ 0.0000e+00, 0.0000e+00, 1.0000e+00]])
Example 2: Inverse on SO(2)
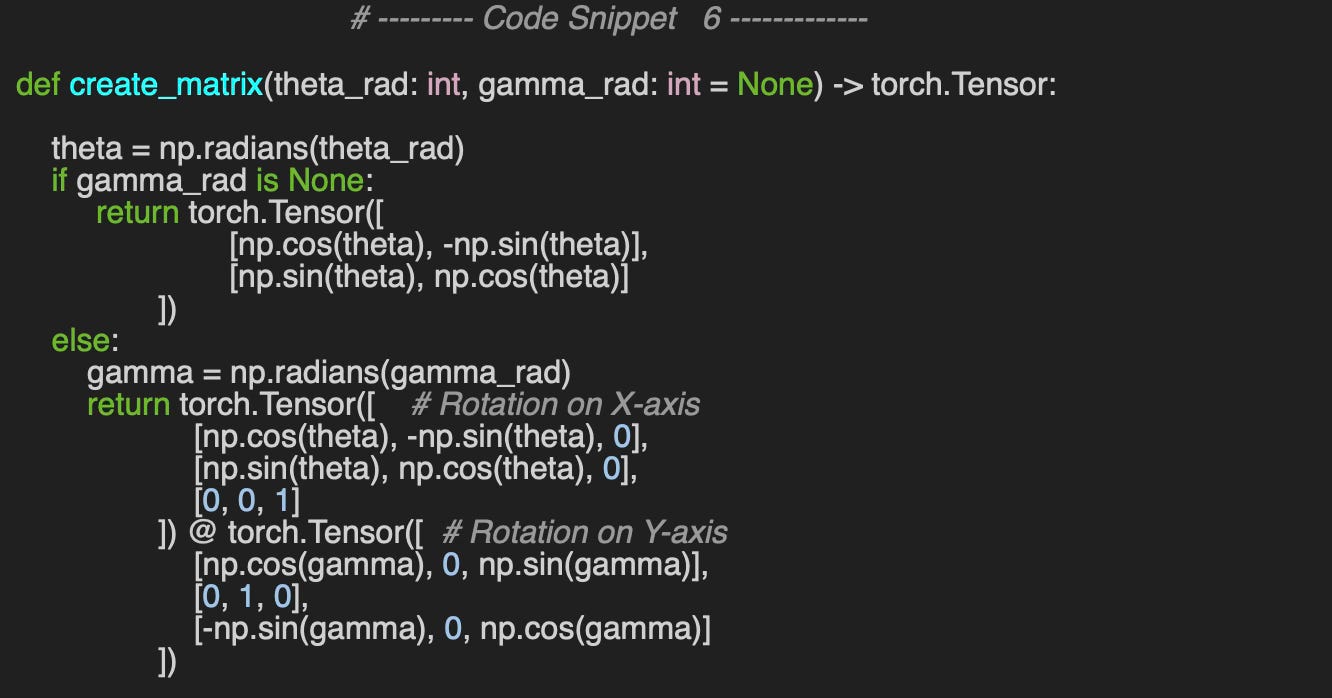
We leverage the method, create_matrix, to generate rotation matrices given angles, described in the Appendix. We also validate the inverse of 2 x 2 rotation R as equal to its transpose. We also validate the algorithm with the identity rotation for fun.
Output:
Rotation:
tensor([[ 6.1232e-17, -1.0000e+00],
[ 1.0000e+00, 6.1232e-17]])
Inverse rotation:
tensor([[ 6.1232e-17, 1.0000e+00],
[-1.0000e+00, 6.1232e-17]])
Identity:
tensor([[1., 0.],
[0., 1.]])
Inverse identity:
tensor([[1., 0.],
[0., 1.]])Example 3: Projection on SO(3)
First we evaluate the projection of a 3x3 rotation matrix generated through a linear combination of so3 basis matrices. Then we project the identity matrix to further validate the computation.
👉 Output
Matrix:
tensor([[ 0.0000, 0.8000, -1.0000],
[-0.8000, 0.0000, 0.5000],
[ 1.0000, -0.5000, 0.0000]])
Projected matrix:
tensor([[-1.2207e-04, 5.8203e-01, -7.2705e-01],
[-5.8185e-01, 1.2207e-04, 3.6377e-01],
[ 7.2736e-01, -3.6389e-01, -2.4414e-04]])
Identity:
tensor([[1., 0., 0.],
[0., 1., 0.],
[0., 0., 1.]])
Projected identity:
tensor([[1., 0., 0.],
[0., 1., 0.],
[0., 0., 1.]])As expected the project of the identity matrix is the identity matrix, a satisfying condition of SO(n) groups.
🧠 Key Takeaways
✅ This article presents four methods for generating SO(n) rotation matrices: QR decomposition, the Geomstats API, angle-based direction instantiation, and linear combinations of basis rotations.
✅ A generic validation mechanism for the Special Orthogonal algebra was implemented and integrated across all operations.
✅ We evaluated the exponential and logarithm maps, along with commonly used operations, for both SO(2) and SO(3) groups.
✅ The Geomstats library equips data scientists with a comprehensive set of tools to explore and implement computations involving Special Orthogonal Groups.
📘 References
geomstats: a Python Package for Riemannian Geometry in Machine Learning N. Miolane, J. Mathe, C. Donnat, M. Jorda, X. Pennec
🛠️ Exercises
Q1: What are the two criteria that determine whether a matrix belongs to the Special Orthogonal Group SO(n)?
Q2: What is the rotation matrix on SO(2) group for the following skew symmetric matrix on so2 Algebra
Q3: Given the rotation matrix:
What is its inverse?
Q4: Can you verify that multiplying an SO(3) rotation matrix by its inverse yields the identity matrix?
💬 News & Reviews
This section focuses on news and reviews of papers pertaining to geometric deep learning and its related disciplines.
Paper Review: An Introduction to Topological Data Analysis: Fundamental and Practical Aspects for Data Scientists F. Chazal and B. Michel - 2021
This article provides a comprehensive yet concise guide to applying Topological Data Analysis (TDA) in data analysis, offering just enough information without overwhelming the reader. TDA is a burgeoning field that utilizes novel tools from algebraic topology and computational geometry to extract significant features from complex data sets.
What I appreciate about the paper is:
Clear definition of the TDA pipeline, which interestingly doesn't rely on Euclidean metrics.
Its accessibility to non-experts, introducing fundamental TDA concepts like metric spaces, simplicial complexes, and Persistent homology in an understandable manner (although I feel that the sections on applying persistent homology in data analysis, feature engineering, and optimizing machine learning architectures could have been more detailed and extensive
The way it illustrates the concept of filtration with practical examples and visual aids.
The application of persistent homology to proteins, demonstrated with Python code and the Gudhi library.
👉 Appendix
Generation of so2 or so3 rotation matrices using angles as arguments
Definition of the basis matrices for so2, so3 and so4 Lie groups, implemented as a private static method.
Patrick Nicolas has over 25 years of experience in software and data engineering, architecture design and end-to-end deployment and support with extensive knowledge in machine learning.
He has been director of data engineering at Aideo Technologies since 2017 and he is the author of "Scala for Machine Learning", Packt Publishing ISBN 978-1-78712-238-3 and Geometric Learning in Python Newsletter on LinkedIn.