Einstein Summation in Geometric Deep Learning

The einsum function in NumPy and PyTorch, which implements Einstein summation notation, provides a powerful and efficient way to perform complex tensor and matrix operations. This function plays a crucial role in two major libraries for geometric deep learning: Geomstats and PyTorch Geometric.

This article explores the various applications and use cases of this essential function.

Table of Contents

1. 🎯 Why this Matters

2. 🎨 Modeling & Design Principles
   Overview

   Numpy einsum

   PyTorch einsum

3. ⚙️ Hands-on with Python

   Environment

   Matrix Operations

   Applications

4. 🧠 Takeaways

5. 📘 References

6. 🛠️ Exercises

7. 💬 News & Reviews

🎯 Why this Matters

Purpose: Many research papers utilize Einstein summation notation to express mathematical concepts concisely. Wouldn't it be useful to have a similar approach or operator available in Python?

Audience: Data scientists and engineers looking to understand or implement the linear algebraic computations that power complex deep learning algorithms.

Value: Learn how to leverage NumPy’s einsum method to efficiently perform complex linear algebra operations, as demonstrated in PyTorch Geometric and the Geomstats Python library.

🎨 Modeling & Design Principles

Overview

The Einstein summation convention is widely used in differential geometry, particularly in fields such as physics, quantum mechanics, general relativity, and geometric deep learning. Two prominent libraries in geometric learning, PyTorch Geometric and Geomstats, heavily rely on Einstein summation for efficient tensor operations.

But what is the Einstein summation?

The Einstein convention implies a summation over a set of indexed terms in a formula ref 1]. Here are some example for Linear Algebra

\(u_{i} = \sum_{j=1}^{n}A_{ij}v_{j}\cong \color{Red} A^{i}_{j}v^{j} \ \ \ \ \color{black} C^{i}_{j} = \sum_{k=1}^{n}A_{ik}B_{kj}\cong \color{Red} (AB)_{ij}\)

The Einstein summation convention is also extensively used in differential calculus. The following formulas represent the divergence, gradient, and Laplacian of a function or vector field [ref 2].

\( \large \nabla .F= \sum_{i=0}^{n} \frac{\partial F^{i}}{\partial x_{i}} \cong \color{Red} \partial_{i}F^{i} \ \ \ \ \color{Black} \nabla f=\sum_{i=0}^{n}\frac{\partial f}{\partial x_{i}} \cong \color{Red} \partial _{i}f \ \ \ \ \ \color{Black} \nabla ^{2}f= \sum_{i=1}^{n}\frac{\partial ^{2}f}{\partial x^{2}_{i}} \cong \color{Red} \partial ^{2}_{i}f\)

Numpy einsum

The numpy.einsum function provides a flexible and efficient way to perform tensor operations using Einstein summation notation [ref 3]. It simplifies operations such as dot products, matrix multiplications, transpositions, outer products or tensor contractions.

The method einsum implements the Einstein summation indices convention with 3 different operational modes.

• Implicit Subscripts: This is the default and simplest format of the function. The sequence of operations is inferred based on the input subscripts.

  Syntax: np.einsum('subscript1, subscript2, ...', tensor1, tensor2)

  Example: np.einsum('ji', t) computes the transpose of np.einsum('ij', t).

• Explicit Subscripts: Some operations may require more specific instruction for processing indices. In this case, the output format is explicitly specified.

  Syntax: np.einsum('subscript1, subscript2, ... -> output', tensor1, tensor2

  Example: np.einsum('ij,jk->ik', a, b) computes the matrix multiplication of a and b.

• Broadcasting: This convenient mode is supported by using ellipsis notation.

  Example: np.einsum('...ii->...i', t) extracts the diagonal along the last two dimensions.

Fig. 1 einsum notation and corresponding Numpy functions for key matrix operations

Example:

The core concept of Geomstats is to incorporate differential geometry principles, such as manifolds and Lie groups, into the development of statistical and machine learning models. Geomstats serves as a practical tool for gaining hands-on experience with geometric learning fundamentals while also supporting future research in the field.

Geomstats relies significantly on Numpy and PyTorch einsum functions. The library associates a back-end computation module, gs to either Numpy or PyTorch.

The following code snippet describes the Geomstats function that change sign of the determinant of a matrix if it is negative.

Geomstats makes extensive use of NumPy and PyTorch's einsum functions for efficient tensor computations. The library utilizes a backend computation module (gs), which can be set to either NumPy or PyTorch, allowing flexible execution.

The following code snippet demonstrates a Geomstats function that adjusts the sign of a matrix's determinant, ensuring it remains positive.

PyTorch einsum

The torch.einsum method in PyTorch provides a flexible and efficient way to perform tensor operations based on Einstein summation notation [ref 4]. It allows for concise, readable, and optimized implementations of dot products, matrix multiplications, outer products, transpositions, and more complex tensor contractions.

As expected, the PyTorch definition follows the same protocol or convention that its counter part in Numpy.

Fig. 2 Einsum notation and corresponding PyTorch functions for tensor operations

Example

The library PyTorch Geometric relies on einsum for implementing complex matrix manipulation. Let’s consider the message function in the forward method for the relational graph attentional operator, (class RGATConv).

The line (1) implements a generalized matrix computation with a dot product as follows:

\(outi[a, c, e] = \sum_{b, d} x_i[a, b, c, d] \cdot w[a, c, d, e]\)

with a summation over the indices b and d while the indices a, c and e defines the shape of the output tensor.

⚙️ Hands-on with Python

Environment

• Libraries: Python 3.12, Numpy 2.2.0, PyTorch 2.5.1, PyTorch Geometric 2.6.1, Geomstats 2.8.0

• Source code is available at GitHub/geometriclearning/util.ein_sum

• To enhance the readability of the algorithm implementations, we have omitted non-essential code elements like error checking, comments, exceptions, validation of class and method arguments, scoping qualifiers, and import statements.

Matrix Operations

The NumPy einsum method offers an elegant alternative to the commonly used @ operator or dedicated NumPy methods.

Matrix multiplication

einsum can be used as an alternative to the Numpy operator @ and matmul method.

The sequence of operations are

1. multiply a and b in a particular way to create new array of products; and then maybe

2. sum this new array along particular axes

3. transpose the axes of the new array in a particular order, if necessary.

[[0.7  2.25]
 [2.   4.75]]

Let’s look at PyTorch implementation of einsum for matrix multiplication

tensor([[ 1.1400, -0.4900, -0.2500],
        [ 0.1300, -0.3000,  0.3700],
        [-0.3600,  0.5700, -0.5100]])

Dot product

Let’s look at the computation of the dot product of two vectors using einsum methods in Numpy and PyTorch.

3.5

Matrix outer product

The NumPy outer method is specifically designed for vector operations. When applied to matrices, the outer product is flattened into a single matrix, requiring reshaping to properly compare results with the einsum function.

This demonstrates another advantage of using einsum, as it avoids the need for reshaping and provides a more intuitive representation of tensor operations.

Outer Product Vectors
[[0.1  2.   1.2 ]
 [0.05 1.   0.6 ]
 [0.2  4.   2.4 ]
 [0.07 1.4  0.84]
 [0.09 1.8  1.08]]

Outer Product Matrices
[[[[ 0.1   2.  ]
   [ 1.2   0.5 ]]
  [[ 0.05  1.  ]
   [ 0.6   0.25]]
  [[ 0.04  0.8 ]
   [ 0.48  0.2 ]]]
 [[[ 0.05  1.  ]
   [ 0.6   0.25]]
  [[-0.03 -0.6 ]
   [-0.36 -0.15]]
  [[ 0.02  0.4 ]
   [ 0.24  0.1 ]]]
 [[[-0.1  -2.  ]
   [-1.2  -0.5 ]]
  [[ 0.04  0.8 ]
   [ 0.48  0.2 ]]
  [[-0.03 -0.6 ]
   [-0.36 -0.15]]]]

Matrix Transpose

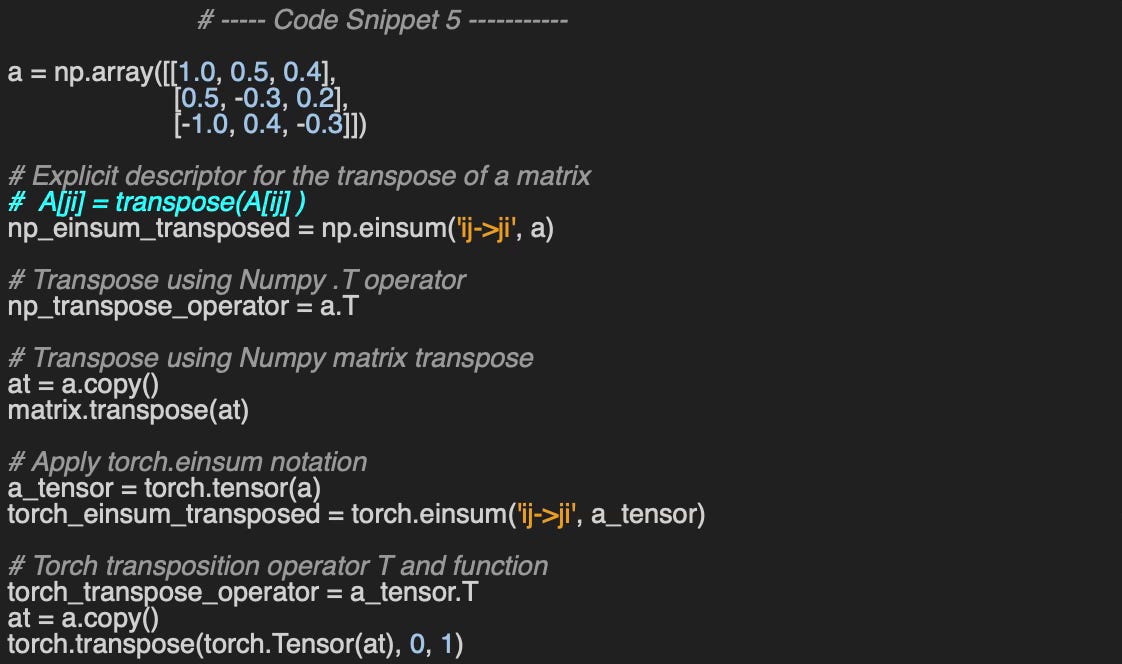
The simplest way to transpose a matrix in both NumPy and PyTorch is by using the .T operator or calling the matrix.transpose and torch.transpose methods

This operation can also be effortlessly performed using einsum, simply by reversing the order of indices.

[[ 1.   0.5 -1. ]
 [ 0.5 -0.3  0.4]
 [ 0.4  0.2 -0.3]]

Matrix Trace

The trace of a square matrix is the sum of its main diagonal elements and can also be interpreted as the sum of some of its eigenvalues. It serves as a linear mapping for any square matrix and remains invariant under transposition, meaning the trace of a matrix equals the trace of its transpose. In NumPy, the trace is easily computed using the trace() method:

The einsum implementation is self-explanatory.

3.99999

Applications

I thought it would be interesting to look at few applications that leverages einsum function.

Neural Network Linear Layer

The linear transformation of a layer of multi-layer perceptron [ref 5] is defined as

\(\textbf{y} = W.\textbf{x} + b \)

with

• W is the weight matrix,

• x is the input vector,

• b is the bias vector,

• y is the output vector.

[2.3  2.46 1.29]

Kalman Filter State Equation

The state transition equation of the Kalman filter [ref 6, 7] is defined as:

\(\widetilde{x}_{k/k-1}=A_{k}.\widetilde{x}_{k-1/k-1} + B_{k}.u_{k} + w\)

with

• x[k]: Estimate state vector at time or step k

• A[k] : State transition matrix (from state x[k-1] to state x[k])

• u[k] : Value of the control variable at step k

• B[k] : Optional control matrix at step k

• w : Process noise covariance matrix

[2.2  1.12]

🧠 Takeways

✅ The Einstein summation notation is extensively used in tensor calculus across various scientific and technical fields, including General Relativity, Differential Geometry, Quantum Mechanics, Molecular Dynamics, and, more importantly, Graph Neural Networks and Geometric Deep Learning.

✅ The einsum function in both NumPy and PyTorch provides a powerful and intuitive way to perform complex matrix and tensor operations with ease.

✅ Two major Python libraries dedicated to geometric learning, Geomstats and PyTorch Geometric, make frequent use of einsum in both PyTorch and NumPy to efficiently handle tensor computations.

📘 References

1. Einstein Summation Notation Course

2. Einstein Summation Notation A. Sengupta

3. Numpy einsum - numpy.org

4. Torch einsum - PyTorch.org

5. Building Multilayer Perceptron Models in PyTorch A. Tam - Machine Learning Mastery

6. Kalman Filter Tutorial KalmanFilter.Net

7. Limitation of Linear Kalman Filter P. Nicolas - Geometric Learning

🛠️ Exercises

• Q1: What is the difference between implicit and explicit subscripts in Einstein summation notation?

• Q2: Can you rewrite the following operations using NumPy's einsum function, given matrices a and b from Code Snippet 1?

  \(c=a@b \ \ (Multiplication) \ \ \ \ and \ \ \ \ d=c^{T} \ \ \ (Tranpose)\)

• Q3: Can you use PyTorch's einsum function to compute the gradient of the function:

  \(\nabla f \ \ \ given \ \ \ \ f(x, y)=x^{2} +y^{3} + 1\)

• Q4: What happens if you attempt to compute the dot product of two vectors of different sizes? (Referencing Code Snippet 3).

• Q5: Can you implement a simple validation function to check whether a matrix transpose is correct?

👉 Answers

💬 News and Reviews

This section focuses on news and reviews of papers pertaining to geometric deep learning and its related disciplines.

Paper review: Machine Learning a Manifold S. Craven, D. Croon, D. Cutting, R. Houtz

---

In quantum physics, the symmetry of experimental data often simplifies many challenges. The researchers utilize neural networks to detect symmetries within a dataset. They define a symmetry V in the context of a transformation f acting on coordinates X within a manifold, where V(x) = V(f(x)). This approach focuses on the manifold's local properties, which helps manage issues arising from data with very high dimensions, as the Lie algebra is situated within the manifold's tangent space.

To achieve this, an 8-layer feed-forward network is employed for interpolating data, predicting infinitesimally transformed fields, and identifying the symmetry. The Keras library is used for this implementation. The neural model is capable of recognizing symmetries in the Lie groups of SU(3), which involves orientation preservation, and SO(8), which relates to Riemannian metric invariance.

Understanding this paper benefits from some background in differential geometry, Lie algebra, and manifolds.

For introduction to manifolds, as reference: https://math.berkeley.edu/~jchaidez/materials/reu/lee_smooth_manifolds.pdf

---

Patrick Nicolas is a software and data engineering veteran with 30 years of experience in architecture, machine learning, and a focus on geometric learning. He writes and consults on Geometric Deep Learning, drawing on prior roles in both hands-on development and technical leadership. He is the author of Scala for Machine Learning (Packt, ISBN 978-1-78712-238-3) and the newsletter Geometric Learning in Python on LinkedIn.