Reusable Neural Blocks in PyTorch & PyG

At some point, we all encounter the challenges of complexity and repetition when building deep learning models. Wouldn't it be beneficial to have pre-packaged modules that can be reused across multiple models and applications?

In this article, we introduce a straightforward approach to organizing and packaging PyTorch components into reusable neural blocks. This first installment outlines a hierarchical structure for neural components, while the next article will focus on the dynamic assembly of deep learning models.

Table of Contents

1. Why this Matters 💬

2. Modeling & Design Principles 🎨

   Overview

   Composite Design Pattern

   Multi-Layer Perceptron Components

   Convolutional Network Components

   Deconvolutional Network Components

   Variational Components

   Graph Neural Network Components

3. Hands-on with Python 💻

   Environment

   Design

   Multi-Layer Perceptron Neural Block

   Convolutional Neural Block

   Deconvolutional Neural Block

   Variational Neural Block

   Message-Passing Graph Neural Block

   Graph Convolutional Neural Block

4. Takeaways 🧠

5. References 📘

6. Exercises 🛠️

7. News & Reviews 📰

Why this Matters 💬

Purpose: Many deep learning models consist of numerous components, often with repeated structures. Developing and evaluating models in PyTorch can be streamlined by utilizing a library of predefined, tested, and reusable components.

Audience: Data scientists and engineers aiming to enhance the readability and reusability of their model implementations.

Value: Gain insights into packaging related neural components in PyTorch into modular, reusable blocks that can be dynamically assembled for efficient model development.

Modeling & Design Principles 🎨

Overview

While this newsletter primarily focuses on Geometric Deep Learning [ref 1] and Graph Neural Networks [ref 2], I believe that reusability and dynamic modeling are fundamental concepts that should be defined and understood across various neural architectures.

I assume the reader has a foundational understanding of neural networks and their key components, which we aim to package.

As suggested by the title, this newsletter extensively utilizes the PyTorch [ref 3] and PyTorch Geometric (PyG) [ref 4] libraries for implementing and evaluating models in Geometric Deep Learning. Consequently, all components introduced in this series will inherit from the torch.nn.Module class.

Composite Design Pattern

Our foundational unit is a neural block which inherits from PyTorch class, Module and encapsulates a set of PyTorch modules as described below.

Fig. 1 Illustration of the architecture of Neural Blocks using the Composite Pattern

Multi-Layer Perceptron Components

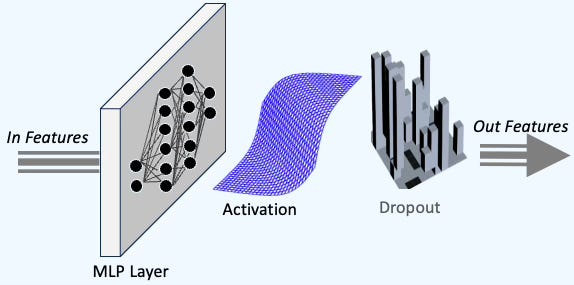
Let's begin with the simplest type of neural network: the Multi-Layer Perceptron (MLP). At its core, an MLP consists of a stack of three key components, as illustrated below:

• A linear layer of neural units

• An optional activation function

• Dropout, commonly used for regularization

Fig. 2 Foundational components of a Multi-Layer Perceptron

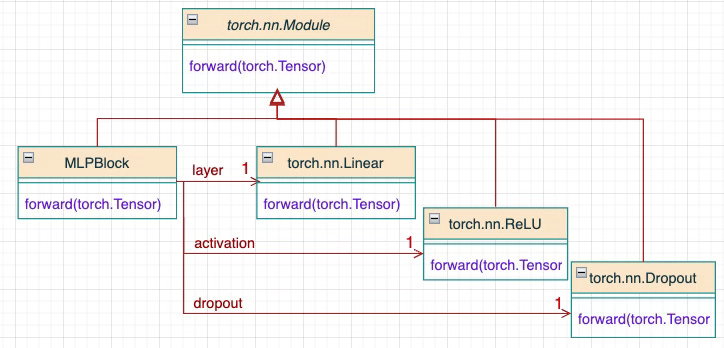
These blocks are repeatedly used and stacked to form the foundation of a Multi-Layer Perceptron, as shown below:

Fig. 3 Class Diagram of a reusable MLP block

Convolutional Network Components

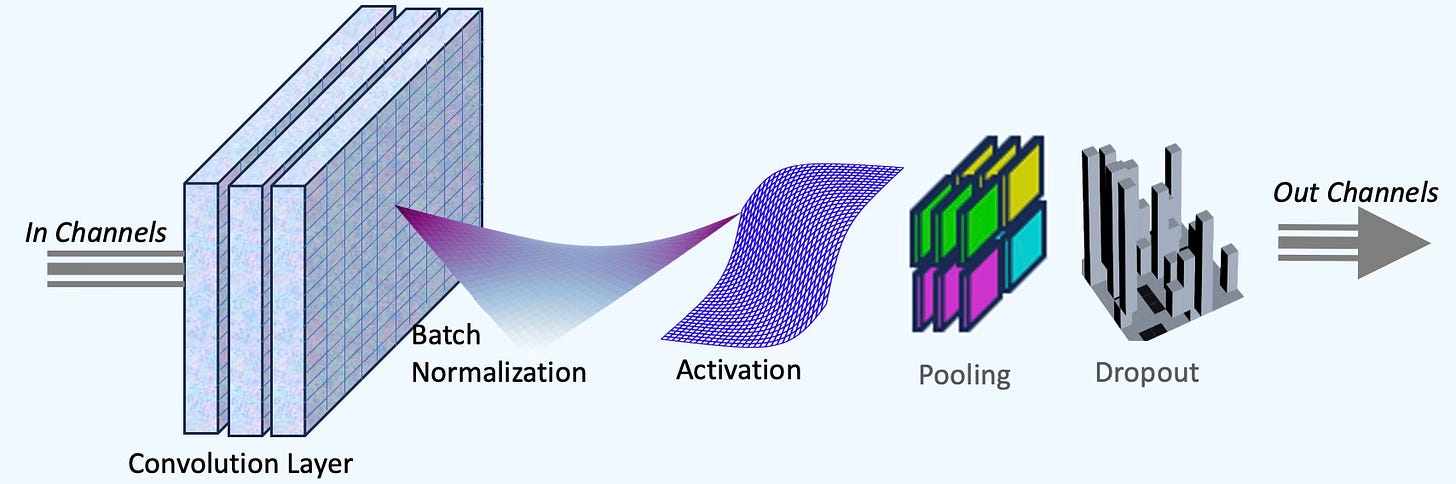
The implementation of Convolutional Neural Networks (CNNs) [ref 5] in PyTorch includes several reusable modules across layers. The fundamental components of a convolutional neural block are:

• Convolutional layer with a kernel filter, stride and padding configuration

• Optional batch normalization

• Activation function

• Pooling module (max or average)

• Optional Dropout for regularization

Fig. 4 Foundational components of a convolutional neural block

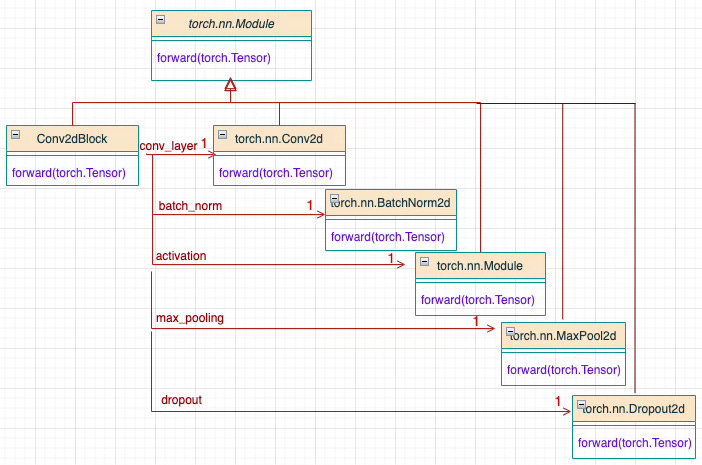
A Convolutional Neural Network (CNN) is constructed by stacking several of these convolutional blocks and incorporating a few fully connected (feedforward) layers, as illustrated below.

Fig. 5 Class Diagram of a reusable 2-dimensional Convolutional Neural Block

Deconvolutional Network Components

Generative models, such as Convolutional Autoencoders and Convolutional Generative Adversarial Networks, utilize a deconvolutional network as a decoder acting as the generative component. Unlike a standard convolutional block, a deconvolutional neural block does not include a pooling module. Since deconvolutional networks naturally upsample data, images, or 3D objects, pooling becomes unnecessary.

Therefore a deconvolutional block contains

1. Deconvolutional layer

2. Optional batch normalization

3. Activation function

4. Dropout regularization module’

Fig. 6 Foundational components of a deconvolutional neural block

📌 The construction of Variational Autoencoders and Generative Adversarial Networks (GANs) using convolutional and deconvolutional layers is detailed in the following article: "Reusability in PyTorch: Dynamic Modeling."

---

Variational Components

In the previous paragraph, we introduced the deconvolutional block as the decoder or generator component of Autoencoders. Variational Autoencoders (VAEs) [ref 6] are a type of generative model that learn to encode input data into a probabilistic latent space and then reconstruct it, while also ensuring the latent space follows a structured probabilistic distribution (typically Gaussian). This structured latent space allows VAEs to generate new, meaningful samples.

The 3 components of a variational AutoEncoders are

• Encoder: Convert input data into a latency space representation modeled by Gaussian distribution

• Probabilistic latent space: Sample from the learned Gaussian distribution using the re-parameterization trick

• Decoder: Reconstruct the original input data

The goal is to encapsulate the distribution related element into a variational neural block consisting of three neural linear layers:

1. Mean of the distribution (Mu)

2. Log variance of the distribution (LogVar)

3. Sampling operation from the Gaussian distribution in the latent space (Sampler)

Fig. 7 Class Diagram UML overview of a reusable variational neural block

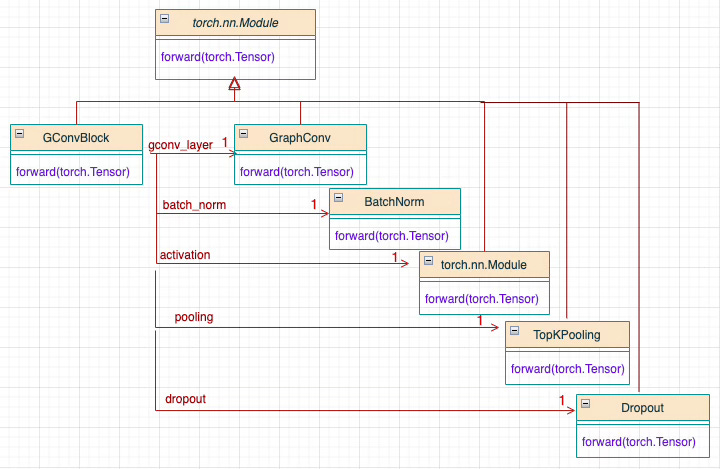
Graph Neural Network Components

Componentizing Graph Neural Networks (GNNs) is particularly challenging due to the diverse implementations in PyTorch Geometric [ref 4], ranging from message-passing and convolutional to attentional models. The goal is to identify the minimal set of attributes that define a graph-based network and are shared across various GNN architectures. The following 5 components are packaged into a Graph Neural Block as illustrated below.

1. Message-passing or convolutional layer

2. Optional batch normalization

3. Activation function

4. Graph Pooling

5. Optional dropout for regularization

Fig. 8 Foundational components of a graph neural block

The 5 components of the Graph Neural Block can be represented using UML:

Fig. 9 Class diagram overview of a Graph Convolutional Neural Block with TopKPooling

Hands-on with Python 💻

Environment

• Libraries: Python 3.12, PyTorch 2.5.1, PyTorch Geometric 2.6.1

• Source code is available at. GitHub.com/patnicolas/GeometricLearning/dl/blocks

• To enhance the readability of the algorithm implementations, we have omitted non-essential code elements like error checking, comments, exceptions, validation of class and method arguments, scoping qualifiers, and import statements.

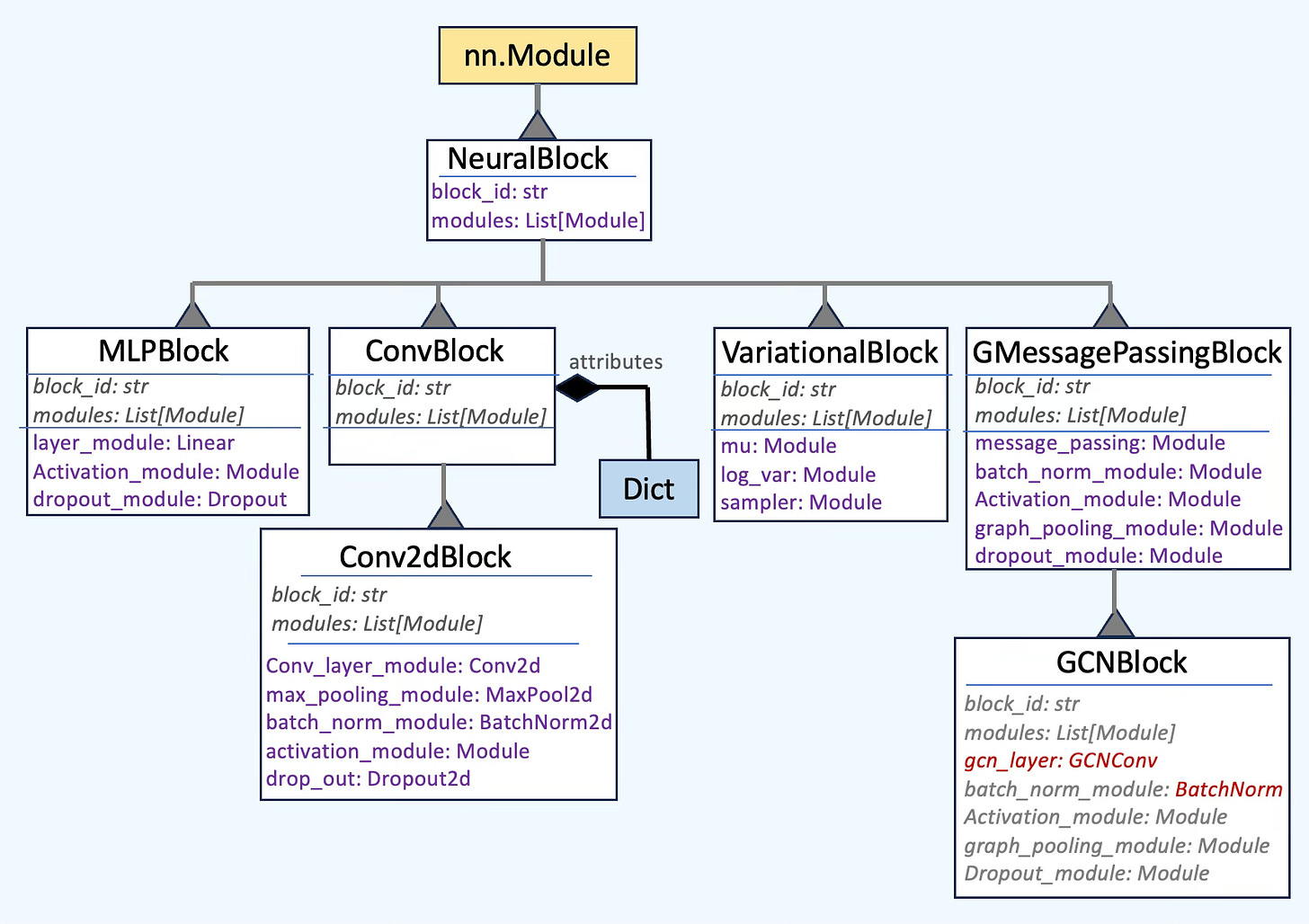
Design

For these neural blocks to be effective and readily usable, their structure and relationships must be properly documented. To achieve this, we utilize a UML-inspired class diagram to systematically track the various neural blocks and their attributes [ref 7].

---

📌 For simplicity, the following class diagram represents only a subset of the neural blocks

---

Fig. 10 Class Diagram software a subset of the neural blocks

At its core, a neural block is defined by its unique identifier and an ordered list of PyTorch modules. Consequently, the constructor of the NeuralBlock class has one attribute:

• `block_id` – A unique identifier used for searching and debugging.

Multi-Layer Perceptron Neural Block

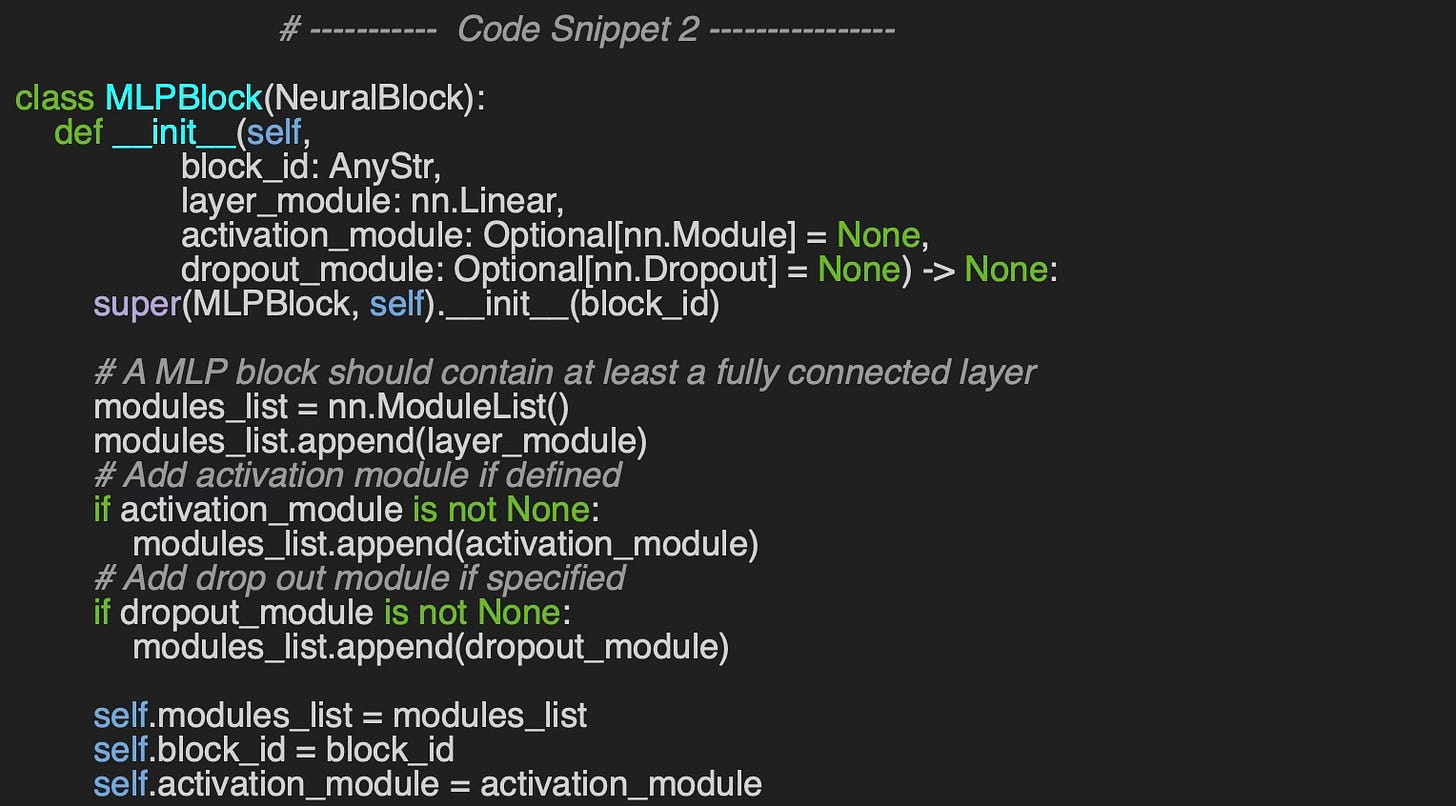
The most fundamental neural block corresponds to the Multi-Layer Perceptron and is implemented in the `MLPBlock` Python class.

This class provides three constructors:

• Default constructor (`__init__`) – Initializes the sequence of modules directly.

• Explicit constructor (`build_from_params`) – Allows for structured creation of the block.

• Dictionary- based constructor (`build`) - Initialize the MLP block from a dictionary of attributes

In the default constructor, the sequence of modules is explicitly initialized, and the activation module is tracked separately, enabling dynamic updates when constructing the complete neural network.

The arguments of the constructor are

• block_id: Simple identifier for the neural block

• layer_module: PyTorch module for the linear transformation y =W.X + b

• activation_module: Optional activation module (i.e. ReLU, Sigmoid, Softmax, )

• dropout_module: Optional Dropout regularization module for training.

We added two supporting method get_in_features and get_out-features to retrieve the dimension of features input and output of the linear layer. These methods are used for validating a sequence of neural blocks in a network.

An alternative constructor, `build_from_params`, provides greater control over the instantiation of a MLP block by allowing explicit configuration of the connected layer in_features , out_features function, and dropout ratio, dropout_p

Finally, a MLP block can be instantiated directly from a dictionary of attributes

   block_attributes = {
            'block_id': 'MyMLP',
            'in_features': in_features,
            'out_features': out_features,
            'activation': nn.ReLU(),
            'dropout': 0.3
        }

Convolutional Neural Block

Packaging the various components of a Convolutional Neural Network (CNN) is more complex. To address this, we create a base class, ConvBlock that standardizes the conversion of different input dimensions for processing.

Additionally, we incorporate an optional dictionary, attributes, to track and validate that the components within a convolutional block are consistent with the shape of input data.

For example, applying convolution to a MRI rendering (dimension 3) typically requires the following set of PyTorch modules.

• A `Conv3d` module for convolution operations.

• A `BatchNorm3d` module for batch normalization.

• A ‘MaxPool3d`

• A `Dropout3d` module for regularization.

---

📌 The attributes dictionary will enable to instantiate automatically deconvolutional neural blocks as described in a future article.

---

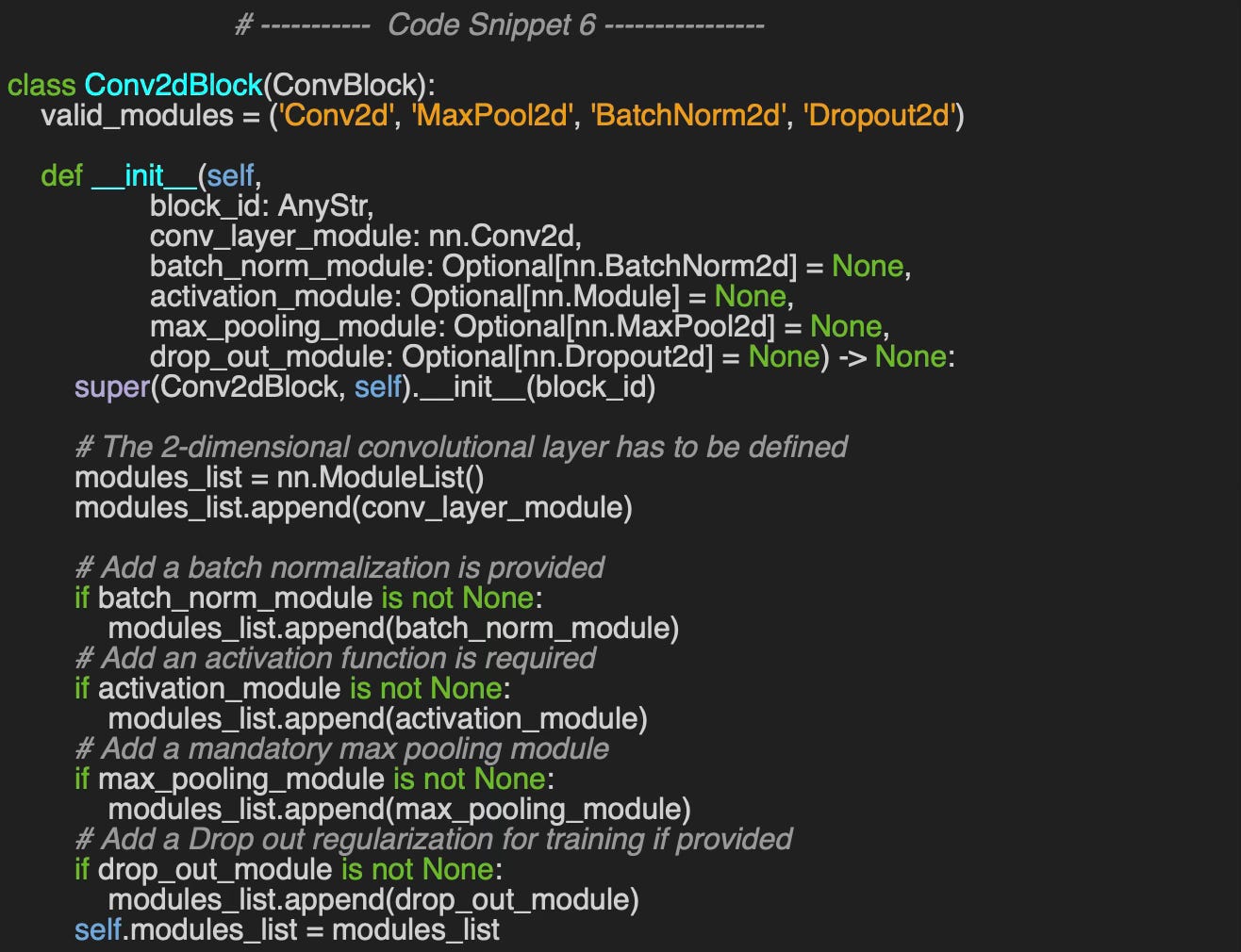
Let's consider the common task of image classification, which requires 2D convolutional components. To address this, we implement the `Conv2dBlock` class, which encapsulates the following:

• A 2D convolution (`Conv2d`) module

• A max pooling module (`MaxPool2d’) for extracting key image features

• An optional 2D batch normalization module, (`BatchNorm2d’)

• An optional activation function

• A dropout module for regularization (`Dropout2d`)

Similar to the feedforward block, the constructor initializes a sequence of PyTorch modules, which are later executed in the forward method.

Once again, the alternative and more descriptive constructor, `build`, offers greater control over the configuration of the convolutional block by allowing explicit specification of each component.

Let’s create a simple 2-dimensional convolutional block.

Example of output:

My_conv_2d:
Modules:
0: Conv2d(1, 32, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), 
          bias=False)
1: BatchNorm2d(32, eps=1e-05, momentum=0.1, affine=True, 
               track_running_stats=True)
2: ReLU()
3: MaxPool2d(kernel_size=2, stride=1, padding=0, dilation=1, 
             ceil_mode=False)
4: Dropout2d(p=0.2, inplace=False)

De-Convolutional Neural Block

The Deconvolutional Network serves as the foundation for decoders in generative models like Autoencoders and Generative Adversarial Networks (GANs), mirroring the structure of convolutional components.

The `DeConv2dBlock` class implements a deconvolutional neural block, utilizing the same modules as the convolutional block, with one key difference—the pooling component is omitted since deconvolutional architectures inherently perform upsampling.

Variational Neural Block

As previously mentioned, Autoencoders and Generative Adversarial Networks (GANs) benefit from reusable feedforward and convolutional blocks. Variational Autoencoders (VAEs), in particular, approximate the latent space using a Gaussian distribution.

The `VariationalBlock` class encapsulates the three key modules responsible for modeling this learned distribution:

• `mu` (mean)

• `log_var` (log variance)

• `sampler` for latent space sampling

Similar to previous neural blocks, the alternative constructor, `build`, enables the definition of the three variational modules by specifying:

• `hidden_dim` – the size of the hidden layer

• `latent_size` – the size of the probabilistic latent space, including mean (`mu`) and log variance (`log_var`)

Message-Passing Graph Neural Block

Finally, we need to implement a wrapper for the key components of a Graph Neural Network (GNN). The design must define the minimal set of attributes that fully characterize a given GNN architecture.

The most generic implementation, `GNNBaseBlock`, includes the following five core components:

• message_passing_module – A generic message-passing module from PyTorch Geometric

• batch_norm_module – An optional batch normalization layer

• activation_module – A standard PyTorch activation function

• graph_pooling_module – A generic graph pooling mechanism

• drop_out_module – An optional dropout layer for regularization

Additionally, we provide an implementation of the `forward` method, which serves as a reference for all subclasses.

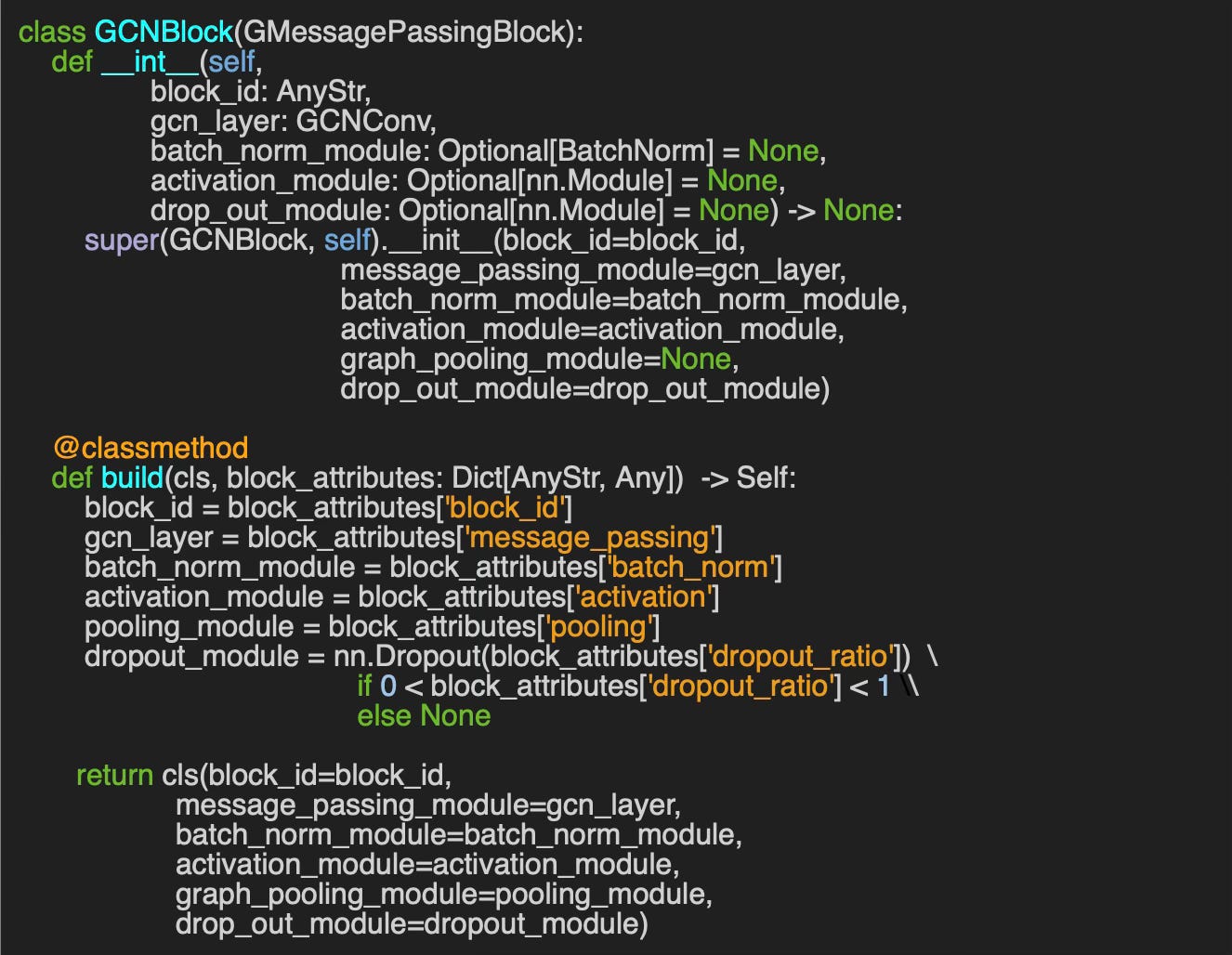
Graph Convolutional Neural Block

Graph Convolutional Neural networks are a special type of GNNs [ref 8]. The `GCNBlock` class serves as the foundational component of a Graph Convolutional Network (GCN) by overriding the message-passing module with `gcn_layer` of type `GCNConv` and specifying `BatchNorm` for the type of batch normalization.

The more descriptive constructor, `build`, enables the creation of a Graph Convolutional Block with just a few key parameters defined in the dictionary of block attributes.

Key Takeways 🧠

✅ Complex deep learning models exhibit several recurring patterns that can be packaged and reused.

✅ Neural blocks can be instantiated using a high-level, modular default constructor or customized through a more descriptive constructor.

✅ The reusability of neural blocks is further enhanced through a combination of class inheritance and object composition.

References 📘

1. Introduction to Geometric Deep Learning P.Nicolas

2. An Introduction to Graph Neural Networks: Models and Applications M. Allamanis - Microsoft Research

3. PyTorch

4. PyTorch Geometric (PyG)

5. An Introduction to Convolutional Neural Networks K. O’Shea, R. Nash

6. An introduction to Variational Autoencoders D. Kingma, M. Welling

7. UML Class Diagram: Unified Modeling Language (UML) Geeks for Geeks

8. Graph Convolutional Networks: Introduction to GNNs M. Labonne - Towards Data Science

Exercises 🛠️

• Q1: Can you implement a convolutional neural block for 3D objects?

• Q2: The `ConvBlock` class, which defines a generic convolutional neural block, includes an optional dictionary of attributes. What is its purpose?

• Q3: Can you write a validation method for a convolutional block using the `attributes` dictionary declared in ConvBlock class?

• Q4: What are the 3 modules of a variational neural block?

• Q5: Which attributes uniquely define a Graph Convolutional Network (GCN) implemented in the `GCNBlock` class?

Answers

News and Reviews 📰

This section focuses on news and reviews of papers pertaining to geometric deep learning and its related disciplines.

Paper review: Autoencoders for discovering manifold dimension and coordinates in data from complex dynamical systems K. Zheng, C. Perez, A. Fox, M. Graham - Dept. of Chemical & Biological Engineering - University of Wisconsin

---

This paper introduces an advanced technique for estimating the dimension of a smooth manifold embedded in Euclidean space using autoencoders.

Dimensionality reduction, whether implicit or explicit, plays a crucial role in improving the predictive accuracy of complex models handling continuous data. The authors propose an Autoencoder-based framework with regularization, incorporating multiple internal linear layers and L2 norm constraints. The exact dimensionality of the feature space is determined by performing singular value decomposition (SVD) on the covariance matrix of the latent Z space within the autoencoder. This method effectively integrates the strengths of both autoencoders and traditional dimensionality estimation approaches.

The technique was tested on 3-dimensional and 8-dimensional manifolds embedded in 4-dimensional and infinite-dimensional Euclidean spaces, respectively, using data generated from nonlinear partial differential equations (PDEs) The results are impressive—the proposed method successfully identified the top 3 (or 8) singular/eigenvalues, surpassing the performance of both Principal Component Analysis (PCA) and standard autoencoders.

A basic understanding of unsupervised learning and dimensionality reduction is recommended for readers.

The Python implementation is available on GitHub (https://github.com/mdgrahamwisc/IRMAE_WD).

---

Patrick Nicolas has over 25 years of experience in software and data engineering, architecture design and end-to-end deployment and support with extensive knowledge in machine learning.
He has been director of data engineering at Aideo Technologies since 2017 and he is the author of "Scala for Machine Learning", Packt Publishing ISBN 978-1-78712-238-3 and Geometric Learning in Python Newsletter on LinkedIn.