Riemannian Manifolds: Foundational Concepts
Intrigued by the idea of applying differential geometry to machine learning but feel daunted? Beyond theoretical physics, the Riemannian manifolds are essential for understanding motion planning in robotics, object recognition in computer vision and visualization.
Table of Contents
🎯 Why this Matters
Purpose: Introduction to smooth and Riemannian manifolds as a core concept of Geometric Deep Learning.
Audience: Data scientists and engineers with basic understanding of machine learning. The reader may benefit from prior knowledge in differential geometry.
Value: Understanding fundamental concepts of data manifolds, including metrics, tangent spaces, geodesics, and intrinsic representations, using Python and the Geomstats library.
🎨 Modeling & Design Principles
This is the first part of our introduction to manifolds and their role in Geometric Deep Learning. This post covers the mathematical foundations, with a focus on differential geometry. The second installment will apply these concepts using the hypersphere.
I highly recommend that readers unfamiliar with the fundamental concepts of differential geometry and their significance in Geometric Deep Learning explore Introduction to Geometric Deep Learning.
Overview
Geometric Deep Learning addresses the difficulties of limited data, high-dimensional spaces, and the need for independent representations in the development of sophisticated machine learning models, including graph-based and physics-informed neural networks. Data scientists face challenges when building deep learning models that can be addressed by geometric, non-Euclidean representation of data Introduction to Geometric Deep Learning: Limitations Current Models
The primary goal of learning Riemannian geometry is to understand and analyze the properties of curved spaces that cannot be described adequately using Euclidean geometry alone
Differential Geometry
The following highlights the advantages of utilizing differential geometry to tackle the difficulties encountered by researchers in the creation and validation of generative models [ref 1].
Understanding data manifolds: Data in high-dimensional spaces often lie on lower-dimensional manifolds. Differential geometry provides tools to understand the shape and structure of these manifolds, enabling generative models to learn more efficient and accurate representations of data.
Improving latent space interpolation: In generative models, navigating the latent space smoothly is crucial for generating realistic samples. Differential geometry offers methods to interpolate more effectively within these spaces, ensuring smoother transitions and better quality of generated samples.
Optimization on manifolds: The optimization processes used in training generative models can be enhanced by applying differential geometric concepts. This includes optimizing parameters directly on the manifold structure of the data or model, potentially leading to faster convergence and better local minima.
Geometric regularization: Incorporating geometric priors or constraints based on differential geometry can help in regularizing the model, guiding the learning process towards more realistic or physically plausible solutions, and avoiding overfitting.
Advanced sampling techniques: Differential geometry provides sophisticated techniques for sampling from complex distributions (important for both training and generating new data points), improving upon traditional methods by considering the underlying geometric properties of the data space.
Enhanced model interpretability: By leveraging the geometric structure of the data and model, differential geometry can offer new insights into how generative models work and how their outputs relate to the input data, potentially improving interpretability.
Physics-Informed Neural Networks: Projecting physics law and boundary conditions such as set of partial differential equations on a surface manifold improves the optimization of deep learning models.
Innovative architectures: Insights from differential geometry can lead to the development of novel neural network architectures that are inherently more suited to capturing the complexities of data manifolds, leading to more powerful models.
Smooth Manifolds
Differential geometry is an extensive and intricate area that exceeds what can be covered in a single article or blog post. There are numerous outstanding publications, including books [ref 2, 3, 4], papers [ref 5] and tutorials [ref 6], that provide foundational knowledge in differential geometry and tensor calculus, catering to both beginners and experts
To refresh your memory, here are some fundamental elements of a manifold:
A manifold is a topological space that, around any given point, closely resembles Euclidean space. Specifically, an n-dimensional manifold is a topological space where each point is part of a neighborhood that is homeomorphic to an open subset of n-dimensional Euclidean space. Examples of manifolds include one-dimensional circles, two-dimensional planes and spheres, and the four-dimensional space-time used in general relativity.
Smooth or Differential manifolds are types of manifolds with a local differential structure, allowing for definitions of vector fields or tensors that create a global differential tangent space.
A Riemannian manifold is a differential manifold that comes with a metric tensor, providing a way to measure distances and angles.
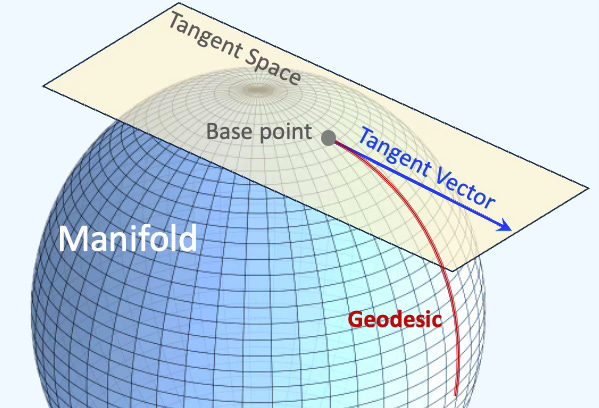
The tangent space at a point on a manifold is the set of tangent vectors at that point, like a line tangent to a circle or a plane tangent to a surface. Tangent vectors can act as directional derivatives, where you can apply specific formulas to characterize these derivatives.
Fig 1 Illustration of a Riemannian manifold with a tangent space
Intuitively, the directional derivative measures how a function changes as you move in a specific direction. The directional derivative
is large and positive, the function is increasing quickly in that direction.
is zero, the function doesn't change in that direction.
is negative, the function is decreasing in that direction.
From the perspective of the manifold (intrinsic view):
If you move in the direction of the steepest ascent (the gradient direction), the directional derivative is at its maximum.
If you move perpendicular to the gradient, the directional derivative is zero (meaning the function isn't changing in that direction).
If you move in the direction of descent, the directional derivative is negative.
Given a differentiable function f, a vector v in Euclidean space Rn and a point x on manifold, the directional derivative in v direction at x is defined as:
and the tangent vector at the point x is defined as
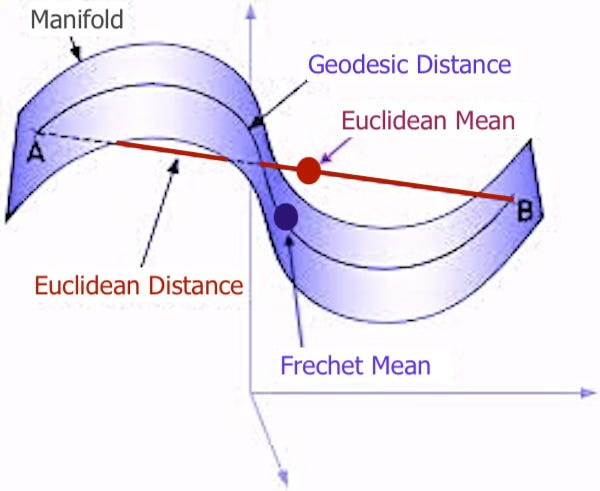
A geodesic is the shortest path (arc) between two points in a Riemannian manifold.
Fig 3 Illustration of manifold geodesics with Frechet mean
Given a Riemannian manifold M with a metric tensor g, the geodesic length L of a continuously differentiable curve f: [a, b] -> M
An exponential map is a map from a subset of a tangent space of a Riemannian manifold. Given a tangent vector v at a point p on a manifold, there is a unique geodesic Gv and a exponential map exp that satisfy:
Lie Groups & Algebras
Lie groups play a crucial role in Geometric Deep Learning by modeling symmetries such as rotation, translation, and scaling [ref 7]. This enables non-linear models to generalize effectively for tasks like object detection and transformations in generative models.
In differential geometry, a Lie group is a mathematical structure that combines the properties of both a group and a smooth manifold. It allows for the application of both algebraic and geometric techniques. As a group, it has an operation (like multiplication) that satisfies 4 axioms:
Closure
Associativity
Identity
Invertibility
A Lie algebra is a mathematical structure that describes the infinitesimal symmetries of continuous transformation groups, such as Lie groups. It consists of a vector space equipped with a special operation called the Lie bracket, which encodes the algebraic structure of small transformations. Intuitively, a Lie algebra is a tangent space of a Lie group.
📌 Lie groups and algebras will be analyzed in details in future posts. Stay tune!
Intrinsic and Extrinsic Geometries
Intrinsic Coordinates
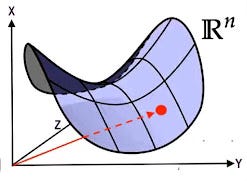
Intrinsic geometry involves studying objects, such as vectors, based on coordinates (or base vectors) intrinsic to the manifold's point. For example, analyzing a two-dimensional vector on a three-dimensional sphere using the sphere's own coordinates.
Intrinsic geometry is crucial in differential geometry because it allows the study of geometric objects as entities in their own right, independent of the surrounding space. This concept is pivotal in understanding complex geometric structures, such as those encountered in general relativity and manifold theory, where the internal geometry defines the fundamental properties of the space.
Here are key points:
Internal Measurements: Intrinsic geometry involves measurements like distances, angles, and curvatures that are internal to the manifold or surface.
Coordinate Independence: Intrinsic coordinates describe points on a geometric object using a coordinate system that is defined on the object itself, rather than in the ambient space.
Curvature: A fundamental concept in intrinsic geometry is curvature, which describes how a geometric object bends or deviates from being flat. The curvature is intrinsic if it is defined purely by the geometry of the object and not by how it is embedded in a higher-dimensional space.
Fig 4. Visualization of intrinsic coordinates of manifold in 3-dimension Euclidean space
Extrinsic Coordinates
Extrinsic geometry studies objects relative to the ambient Euclidean space in which the manifold is situated, such as viewing a vector on a sphere's surface in three-dimensional space.
Extrinsic geometry in differential geometry deals with the properties of a geometric object that depend on its specific positioning and orientation in a higher-dimensional space. It is concerned with how the object is embedded in this surrounding space and how it interacts with the ambient geometry. It contrasts with intrinsic geometry, where the focus is on properties that are independent of the ambient space, considering only the geometry contained within the object itself. Extrinsic analysis is crucial for understanding how geometric objects behave and interact in larger spaces, such as in the study of embeddings, gravitational fields in physics, or complex shapes in computer graphics.
Here’s what extrinsic geometry involves:
Embedding: Extrinsic geometry examines how a lower-dimensional object, like a surface or curve, is situated within a higher-dimensional space.
Extrinsic Coordinates: These are coordinates that describe the position of points on the geometric object in the context of the larger space.
Normal Vectors: An important concept in extrinsic geometry is the normal vector, which is perpendicular to the surface at a given point. These vectors help in defining and analyzing the object's orientation and curvature relative to the surrounding space.
Curvature: Extrinsic curvature measures how a surface bends within the larger space.
Projection and Shadow: Extrinsic geometry also looks at how the object projects onto other surfaces or how its shadow appears in the ambient space.
Fig. 5 Visualization of extrinsic coordinates in 3-dimension Euclidean space
🧠 Key Takeaways
✅ The manifold is a fundamental concept in differential geometry, allowing data scientists to model highly non-linear structures.
✅ Manifolds possess a local Euclidean structure known as the tangent space, where linear algebra, tensor computations, calculus, and standard machine learning algorithms remain applicable.
✅ Mapping between the tangent space and the Riemannian manifold is achieved through the exponential map (to the manifold) and the logarithm map (from the manifold).
✅ Data points, vectors, and tensors can be expressed using either intrinsic coordinates relative to the manifold at a specific point or extrinsic coordinates relative to the ambient Euclidean space in which the manifold is embedded.
📘 References
Differential Geometric Structures W. Poor - Dover Publications, New York 1981
Tensor Analysis on Manifolds R Bishop, S. Goldberg - Dover Publications, New York 1980
Introduction to Smooth Manifolds J. Lee - Springer Science+Business media New York 2013
Introduction to Lie Groups and Lie algebras - A Kirillov. Jr - SUNNY at Stony Brook
🛠️ Exercises
Q1: How would you intuitively define a directional derivative?
Q2: In a manifold, does the Euclidean mean of two data points (i.e., the midpoint between them) necessarily lie on the manifold?
Q3: What is the difference between the exponential map and the logarithm map?
Q4: When analyzing a low-dimensional structure such as a manifold, Lie group, or embedding within a higher-dimensional Euclidean space, which coordinate system should be used?
1) Intrinsic coordinates 2) Extrinsic coordinates
Q5: What are the four axioms that a Lie group must satisfy?
Q6: How would you intuitively define a Lie algebra?
👉 Answers
💬 News & Reviews
This section focuses on news and reviews of papers pertaining to geometric deep learning and its related disciplines.
Paper review Algebra, Topology, Differential Calculus, and Optimization Theory For Computer Science and Machine Learning J. Gallier, J. Quaintance - Dept. of Computer and Information Science - University of Pennsylvania
I discovered a remarkably thorough review of all the mathematics essential for machine learning. This review is well-articulated, making it accessible even for those less enthusiastic about mathematics (no need to bring out your dissertation). Spanning over 2100 pages, the paper encompasses a wide range of algorithms, from fundamental linear algebra, dual space, and eigenvectors to more advanced topics like tensor algebra, affine geometry, topology, homologies, kernel models, and differential forms.
The structure of the paper allows for independent topic exploration. For instance, you can jump right into the chapter on soft-margin support vector machines without needing to go through the preceding chapters. This makes the paper an invaluable resource for anyone seeking a comprehensive mathematical foundation in machine learning.
The index and bibliography are both extensive and detailed. However, a minor drawback is that the only coding examples provided are in Matlab, with no Python implementations.
Patrick Nicolas is a software and data engineering veteran with 30 years of experience in architecture, machine learning, and a focus on geometric learning. He writes and consults on Geometric Deep Learning, drawing on prior roles in both hands-on development and technical leadership. He is the author of Scala for Machine Learning (Packt, ISBN 978-1-78712-238-3) and the newsletter Geometric Learning in Python on LinkedIn.