Block by block: Rethinking Deep Learning Architecture
Constructing and configuring complex neural networks using PyTorch modules can be challenging and prone to errors. This article applies decades of software engineering best practices, focusing on reusability and design patterns, to enable the efficient creation, modification, and reuse of neural networks.
Table of contents
What this Matters 💬
Purpose: Many deep learning models share common neural components and architectural patterns. Streamlining model development and evaluation in PyTorch can be achieved by leveraging a library of predefined, tested, and reusable components, along with software design patterns [ref 1].
Audience: Data scientists and machine learning engineers building diverse neural network architectures who would benefit from improved reusability and modularity.
Value: Gain insights into how to assemble, validate, and optimize neural networks using reusable neural blocks and design patterns.
Modeling & Design Principles 🎨
Overview
This article is a follow up on our introduction to Reusable Neural Blocks in PyTorch [ref 2] and assume basic understanding of neural blocks.
Configuring complex neural networks can be time-consuming and error-prone. Decades of advancements in software engineering have demonstrated the importance of reusability and design patterns, as seen in Object-Oriented Programming (OOP) techniques [ref 3].
There are two primary approaches to constructing neural networks using reusable components:
Neural Blocks Approach (as introduced in Reusable Neural Blocks in PyTorch & PyG). This method, implemented by the default constructor of a model, involves encapsulating related PyTorch modules into neural blocks, which are then assembled into a complete neural network.
Builder Pattern Approach. Utilizes a structured Builder pattern to create and initialize a neural network, ensuring modularity and flexibility.
Assembly
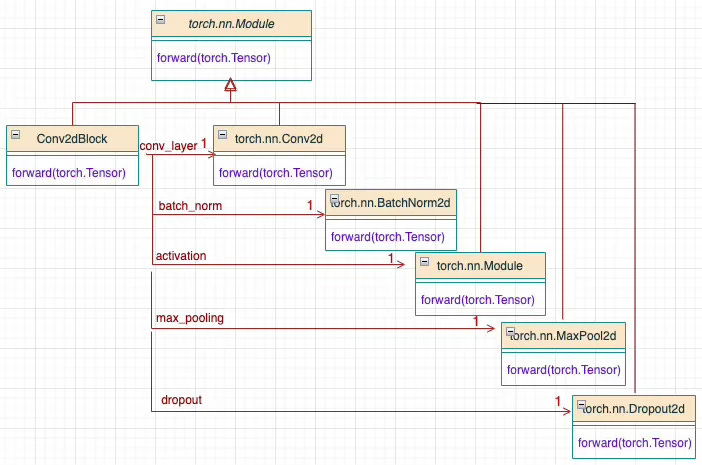
This approach is simple and intuitive. Predefined neural blocks are passed as arguments to the class implementing the network. The convolutional neural block is described in a previous article Reusable Neural Blocks in PyTorch & PyG
Fig. 1 Illustration of reusable 2-dimensional convolutional Neural Block
For example, a convolutional network is instantiated within the __init__ method of its corresponding class.
Fig. 2 Assembly of a 2-dimensional convolutional neural network using neural blocks
The following code snippet is a direct implementation of the assembly.
Builder Pattern
The builder pattern has been widely used in software engineering to assemble complex structures from a set of components [ref 1, 4].
The Builder Pattern is a creational design pattern used for constructing complex objects step by step. It allows you to create different representations of an object while keeping the construction process the same. Its main benefit is to separate the logic of building an object from its representation, making the code easy to read and support different representations.
Fig. 3 Builder pattern applied to the Multi-layer Perceptron
The following image illustrates the application of the builder pattern to our previous 2-dimensional convolutional neural network example.
Fig 4 Instantiation of a 2-dimensional convolutional networks using a Builder pattern
Let’s defined a very generic builder class that generate dynamically an abstract Neural model.
Configuration Validation
Configuring a neural network can be error-prone, making automated validation of parameters a valuable time-saving solution.
For example, in a 2-dimensional convolutional neural network, the number of output channels in one convolutional layer must match the input channels of the next layer, including its corresponding batch normalization module. Moreover the size of an image in various stage of the convolutional network has to comply with the configuration of filter and pooling modules.
For a input data of width W[in] and high H[in], a padding p, a kernel size k and a stride s, the dimension of the output data is defined as
The same validation process applies to deconvolutional layers for a decoder.
📌 Most commonly used datasets relies on resized images with W[in] = H[in]
Transposition
We are now exploring ways to further simplify and automate the configuration of complex neural networks.
Generative models, such as Autoencoders and Generative Adversarial Networks (GANs), utilize an encoder-decoder pair, where the decoder mirrors the encoder.
For example, let's examine a Variational Convolutional Autoencoder (VAE) [ref 5] designed to classify MNIST digits, structured with the following PyTorch modules:
0: Conv2d(3, 8, kernel_size=(3, 3), stride=(1, 1))
1: BatchNorm2d(8, eps=1e-05, momentum=0.1, affine=True,
track_running_stats=True)
2: ReLU()
3: MaxPool2d(kernel_size=1, stride=1, padding=0, dilation=1,
ceil_mode=False)
4: Dropout2d(p=0.25, inplace=False)
5: Conv2d(8, 16, kernel_size=(3, 3), stride=(1, 1))
6: BatchNorm2d(16, eps=1e-05, momentum=0.1, affine=True,
track_running_stats=True)
7: ReLU()
8: MaxPool2d(kernel_size=1, stride=1, padding=0, dilation=1,
ceil_mode=False)
9: Dropout2d(p=0.25)
10: Mean-Linear(in_features=9216, out_features=16, bias=True)
11: LogVar-Linear(in_features=9216, out_features=16, bias=True)
12: Sampler-Linear(in_features=16, out_features=9216, bias=True)
13: ConvTranspose2d(16, 8, kernel_size=(3, 3), stride=(1, 1),
bias=False)
14: BatchNorm2d(16, eps=1e-05, momentum=0.1, affine=True,
track_running_stats=True)
15: ReLU()
16: Dropout2d(p=0.25, inplace=False)
17: ConvTranspose2d(8, 3, kernel_size=(3, 3), stride=(1, 1), bias=False)
18: BatchNorm2d(8, eps=1e-05, momentum=0.1, affine=True,
track_running_stats=True)
19: ReLU()
20: Dropout2d(p=0.25)For clarity, let's visually represent the input and output channel dimensions for each layer in both the encoder (convolutional layers) and decoder (deconvolutional layers).
Fig. 5 Layout input and output channels for a variational convolutional network
With all other configuration parameters remaining the same, the distribution of input channels in the decoder mirrors that of the encoder. This symmetric structure allows for the automatic generation of the decoder from the encoder—an operation we refer to as Transposition.
Hands-on with Python 💻
Environment
Libraries: Python 3.12, PyTorch 2.5.1, PyTorch Geometric 2.6.1
Source code is available at. GitHub.com/patnicolas/GeometricLearning/dl/model
To enhance the readability of the algorithm implementations, we have omitted non-essential code elements like error checking, comments, exceptions, validation of class and method arguments, scoping qualifiers, and import statements.
Neural Models & Builders
Class Library
As mentioned earlier, our neural models are structured as a hierarchy of PyTorch modules to promote reusability. The strategy illustrated below aims to strike a balance between inheritance and composition. Depending on the application, one can design a library that leans more toward composition or inheritance to best suit specific needs.
Fig. 5 Example of class hierarchy of neural networks using PyTorch modules
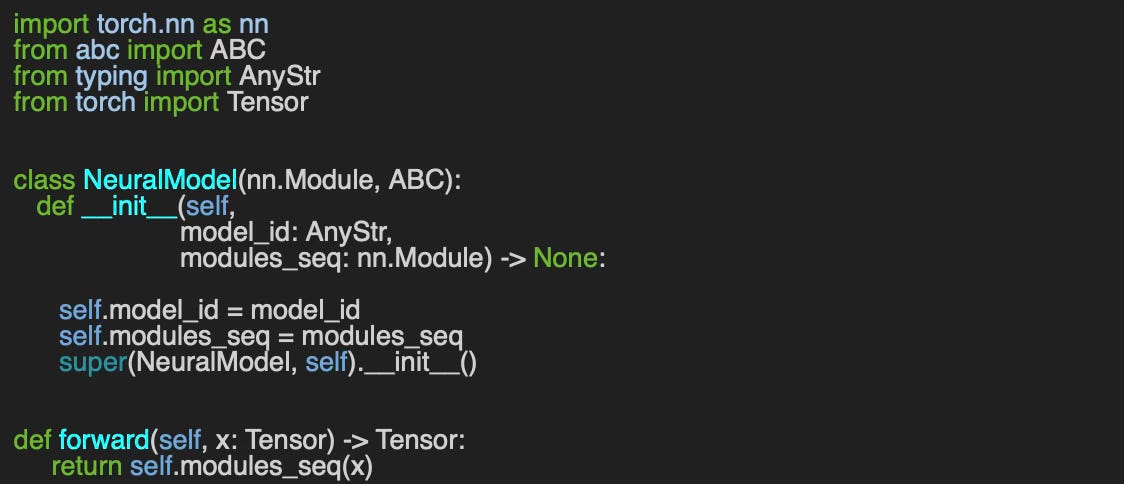
Here is an implementation of the base class, NeuralModel, that takes two arguments:
model_id: Identifier for the model
modules_seq: Ordered sequence of PyTorch modules
The `forward` method, invoked via `__call__`, delegates the execution flow across the PyTorch modules.
Each neural network has a corresponding builder that inherits attributes from the abstract class `NeuralBuilder`. The `set` method enables a subclass to dynamically update the list of attributes as needed.
We now demonstrate the instantiation, dynamic construction, validation, and transposition of Multi-Layer Perceptrons and Convolutional Neural Networks.
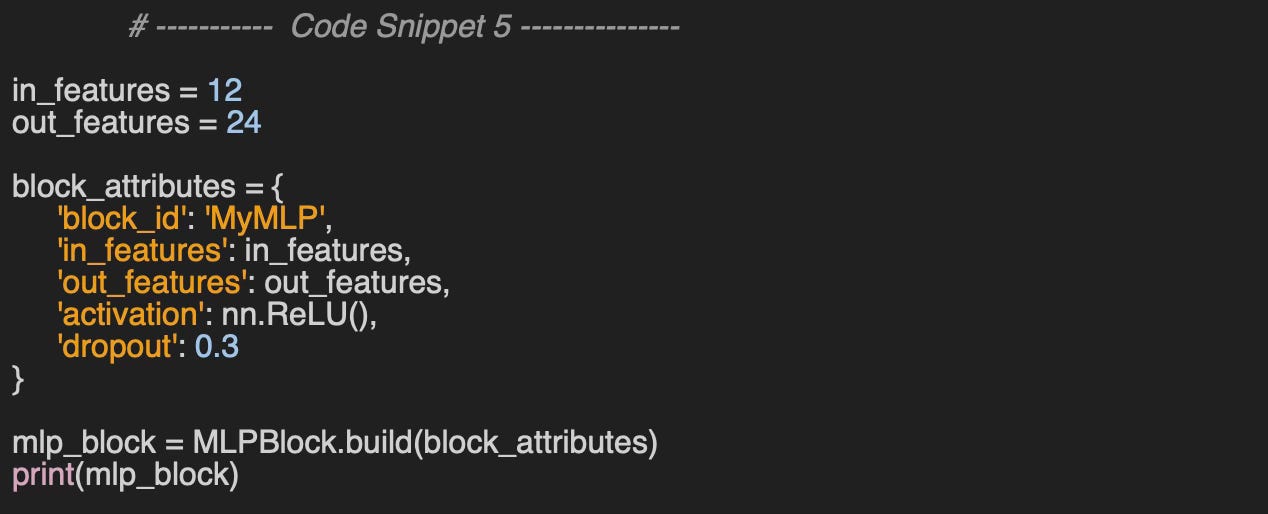
Multi-Layer Perceptron
Let’s write the skeleton code for the creation, validation and transposition of a Multi-Layer Perceptron (MLP)
Model
We begin by instantiating a Multi-Layer Perceptron network, MLPModel, specifying its identifier, model_id, and a list of MLP neural blocks, neural_blocks. Ultimately, the constructor generates the ordered sequence of PyTorch modules.
Builder
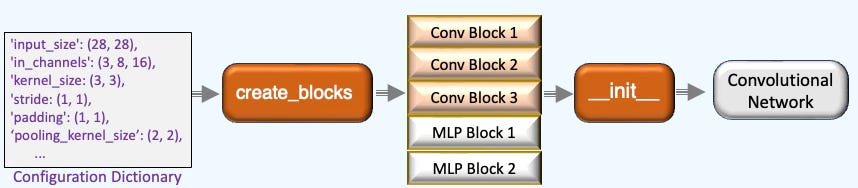
The Builder pattern, implemented through the class MLPBuilder, allows us to directly define the configuration of the artificial neural network using a set of configuration attributes. The Multi-Layer Perceptron model is constructed in three key steps:
Generate MLP neural blocks from a dictionary of attributes.
Validate the configuration to ensure correctness.
Instantiate the network model as an MLPModel.
This simplified builder assumes that the activation and dropout modules remain consistent across all layers of the MLP and have arbitrary default values.. For a more customized architecture, the __create_blocks method can be overridden to incorporate a wider range of configuration parameters. For instance, a batch normalization parameter could be added for training.
📌📌
The parameter output_activation allows for overriding the default activation module for the specific task (classification, regression, ).
The source code for the method, __create_blocks is available on GitHub for a 2-dimensional convolutional network github.com/patnicolas/geometriclearning/dl/model/conv_2d_model.py and a Multi Layer Perceptron: github.com/patnicolas/geometriclearning/dl/model/mlp_model.py
Here is a very simple Multi-Layer Perceptron configuration:
Model: test1
Modules:
0: Linear(in_features=8, out_features=16, bias=False)
1: ReLU()
2: Linear(in_features=16, out_features=16, bias=False)
3: ReLU()
4: Linear(in_features=16, out_features=1, bias=False)
5: Softmax(dim=None)Validation
Next, we validate the architecture of the MLP by ensuring that the number of output features from one layer correctly matches the number of input features for the subsequent layer.
Transposition
Finally, we create a MLP that mirrors the original architecture by simply reversing the order of the neural blocks.
Convolutional Networks
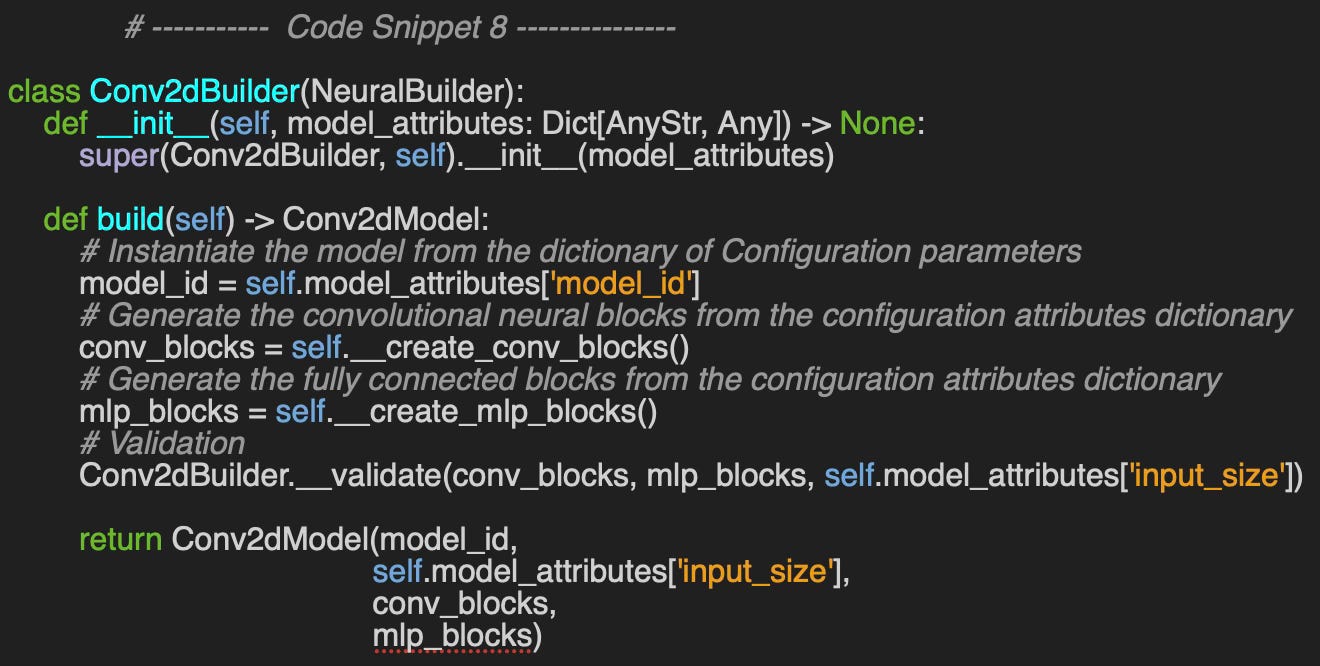
Operations on convolutional neural networks are more complex than those on multi-layer perceptrons, and this complexity extends to instantiation, validation, and transposition.
Let's examine the 2-dimensional convolutional network, implemented in the Conv2dModel class. This network is fully defined by the following attributes:
input_size - Specifies the size of the input data (height and width).
conv_blocks - A list of 2D convolutional neural blocks.
mlp_blocks - An optional list of MLP blocks.
Similar to the MLP model, the constructor constructs an ordered sequence of PyTorch modules to define the network architecture
Builder
The Conv2Builder class implements the Builder Pattern for convolutional networks, using a predefined list of attribute keys. The dictionary of configuration parameters (model_attributes) serves as input to the build method and is somewhat flexible.
Depending on the level of detail required, multiple builders can be designed with varying degrees of granularity. The implementation below assumes that kernel size, stride, and padding remain consistent across all convolutional layers, which may not be sufficiently precise for certain applications.
📌 The implementation of the two methods __create_conv_blocks to assemble the convolutional blocks and __create_mlp_blocks to generate the fully connected blocks are available at github.com/patnicolas/geometriclearning/dl/model/conv_2d_model.py
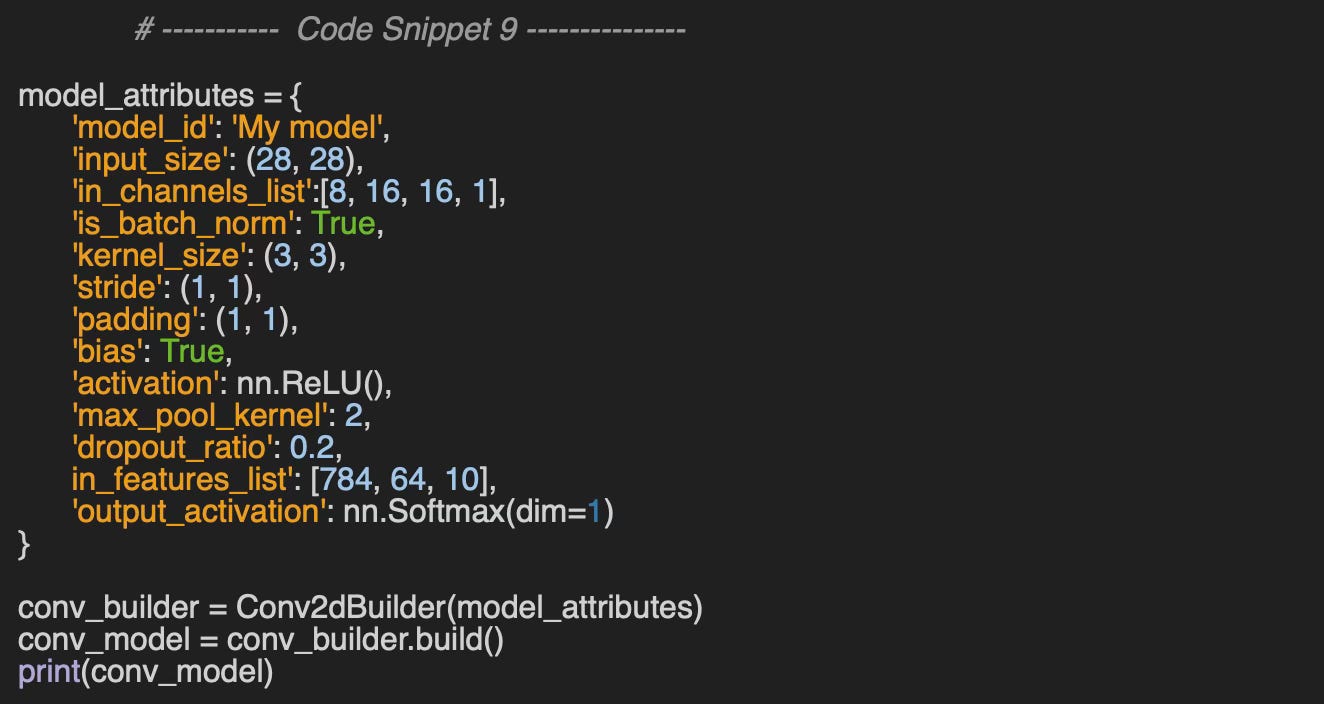
Let’s see how it works in practice by building a 2-dimensional convolutional model to classify digits from MNIST datasets with image size 28x28. The model has 3 convolutional layers with batch normalization, activation and max pooling modules, followed by 2 fully connected layers.
Output:
0: Conv2d(8, 16, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1),
bias=False)
1: BatchNorm2d(16, eps=1e-05, momentum=0.1, affine=True,
track_running_stats=True)
2: ReLU()
3: MaxPool2d(kernel_size=2, stride=1, padding=0, dilation=1,
ceil_mode=False)
4: Dropout2d(p=0.2, inplace=False)
5: Conv2d(16, 16, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1),
bias=False)
6: BatchNorm2d(16, eps=1e-05, momentum=0.1, affine=True,
track_running_stats=True)
7: MaxPool2d(kernel_size=2, stride=1, padding=0, dilation=1,
ceil_mode=False)
8: Dropout2d(p=0.2, inplace=False)
9: Conv2d(16, 32, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1),
bias=False)
10: BatchNorm2d(32, eps=1e-05, momentum=0.1, affine=True,
track_running_stats=True)
11: MaxPool2d(kernel_size=2, stride=1, padding=0, dilation=1,
ceil_mode=False)
12: Dropout2d(p=0.2, inplace=False)
13: Flatten(start_dim=1, end_dim=-1)
14: Linear(in_features=625, out_features=64, bias=False)
15: Dropout(p=0.2, inplace=False)
16: Linear(in_features=64, out_features=10, bias=False)
17: Softmax(dim=1)
18: Dropout(p=0.2, inplace=False)The number of nodes in the first fully connected layer (1D layer), set to 625, is determined by flattening the output of the final convolutional layer and applying the scaling formula outlined in the Configuration Validation section.
Validation
The validation process for the convolutional network configuration consists of two steps:
Validate the structure of convolutional layers using Conv2dBuilder.__validate_conv
Validate the arrangement of feedforward layers, as discussed in the previous section, using MLPBuilder.validate.
📌📌
Although the validation of the layout of the convolutional layers is implemented as a method of Conv2dBuilder class, it applies to 1 and 3 dimensional convolutional networks.
The implementation of the validation of the 2-dimensional convolutional network is available at github.com/patnicolas/geometriclearning/dl/model/conv_2d_model.py
Transposition
The transposition process, implemented in the transpose method of Conv2dModel, constructs a mirrored version of the original convolutional network by:
Transposing each Convolutional Neural Block.
Reversing the order of convolutional blocks.
Instantiating a 2-dimensional Deconvolutional Network.
Takeways 🧠
✅ Data scientists can apply reusability and configurability techniques that have been widely used in software engineering for years.
✅ Neural networks can be constructed from reusable neural blocks.
✅ The Builder Pattern provides a structured approach to simplify and automate the creation of complex neural networks.
✅ Transposition enables the automatic generation of decoders from encoders in generative models, such as Variational Autoencoders (VAEs).
References 📘
Design Patterns: Elements of Reusable Object-Oriented Software - E. Gamma, R. Helm, R. Johnson, J. Vlissides - Addison-Wesley Publishing 1995
Reusable Neural Blocks in PyTorch & PyG P Nicolas
Design Pattern: Builder Tutorials Point
Introduction to Variational Autoencoders D. Kingma, M. Welling
Exercises 🛠️
Q1: Can you explain the Builder Pattern?
Q2: What is the purpose of transposing a neural network?
Q3: Can you write a function, output_size, to compute the size of the output of an input of an image from the convolutional block with a kernel_size, padding and stride, given the size, input_size = (w, h) of the input data?
Q4: Can you implement the __create_blocks method for the builder of a Multi-Layer Perceptron, (class MLPBuilder) using the dictionary of configuration parameters, attributes, initialized in Code Snippet 4?
News & Reviews 📰
This section focuses on news and reviews of papers pertaining to geometric deep learning and its related disciplines.
Paper review: Variational Transformer Autoencoder with Manifolds Learning P. Shamsolmoali, M. Zareapoor, H. Zhou, D. Tao, Fellow, X. Li - IEEE
The paper illustrates how the Riemann metric effectively addresses the challenges of modeling non-linear latent spaces by interpolating between input data samples along geodesics. The researchers have developed a variational autoencoder that incorporates a spatial transformer as the encoder to map the latent space model onto a Riemann manifold.
The goal is to refine the variational auto-encoder to calculate the geodesic distances between input data points, utilizing the Riemann metric tensor, and to delineate a semantic feature/latent space. The encoded transformer component is responsible for calculating the prior in the latent space. Importantly, this new model does not necessitate any modifications to the existing loss function (ELBO) or the training methodology.
Implemented in PyTorch, the model consists of four convolutional layers, two linear reshaping layers, and fifty latent variables. It has been evaluated using a variety of image sets, including grayscale images (such as MNIST and FashionMNIST) and color, natural images (such as CelebA and CIFAR-10). The proposed model demonstrates substantial improvements in image reconstruction.
Note: The paper assumes knowledge of differential geometry and generative models. The source code is available on GitHub.
Patrick Nicolas has over 25 years of experience in software and data engineering, architecture design and end-to-end deployment and support with extensive knowledge in machine learning.
He has been director of data engineering at Aideo Technologies since 2017 and he is the author of "Scala for Machine Learning", Packt Publishing ISBN 978-1-78712-238-3 and Geometric Learning in Python Newsletter on LinkedIn.