Insights into Logistic Regression on Riemannian Manifolds
Traditional linear models in machine learning, such as logistic regression, struggle to grasp the complex characteristics of data in very high dimensions. One type of manifold, the Symmetric Positive Definite (SPD) matrices improve the output quality of logistic regression by enhancing feature representation in a lower-dimensional space.
🎨 Modeling & Design Principles
Exponential & Logarithmic Maps
🛠️ Exercises
🎯 Why this Matters
Purpose: Address the limitations of a linear model such as the logistic regression in an Euclidean space
Audience: Data scientists and engineers with basic understanding of machine learning and linear models. The reader may benefit from prior knowledge in differential geometry.
Value: Learn to implement and validate a binary logistic regression classifier on SPD manifolds using affine invariance and log Euclidean metrics.
🎨 Modeling & Design Principles
Overview
The primary goal of learning Riemannian geometry is to understand and analyze the properties of curved spaces that cannot be described adequately using Euclidean geometry alone.
Using logistic regression for classification on low-dimensional data manifolds offers several benefits:
Simplicity and interpretability: The model provides clear insights into the relationship between the input features and the probability of belonging to a certain class.
Efficiency: On low-dimensional manifolds, logistic regression is computationally efficient.
Good performance in linearly separable cases: The logistic regression performs exceptionally well if the data in the low-dimensional manifold is linearly separable.
Robustness to overfitting: In lower-dimensional spaces, the risk of a simpler model such as the logistic regression to overfit is generally reduced.
Support for non-linear boundaries: Although linear, the logistic regression can handle non-linear boundaries in low-dimensional space than Euclidean space.
This article relies on the Symmetric Positive Definite (SPD) Lie group of matrices as our manifold for evaluation. We will introduce, review or describe:
Logistic regression as a binary classifier
SPD matrices
Logarithms and exponential maps on manifolds
Riemannian metrics associated to SPD
Implementation of binary logistic regression using Scikit-learn and Geomstats Python libraries
Verification using randomly generated SPDs and cross-validation.
Logistic Regression
Let's review the ubiquitous binary logistic regression. For a set of two classes C = {0, 1} the probability of predicting the correct class given a features set x and a model weights w is defined by sigmoid, sigm transform:
The binary classifier is then defined for class C1 and C2 as
For an introduction to basic logistic regression and its implementation for beginners, check out this detailed guide: Logistic Regression Explained and Implemented in Python (ref 6).
Manifolds
To refresh your memory, here are some fundamental elements of a manifold:
A manifold is a topological space that, around any given point, closely resembles Euclidean space. Specifically, an n-dimensional manifold is a topological space where each point is part of a neighborhood that is homeomorphic to an open subset of n-dimensional Euclidean space. Examples of manifolds include one-dimensional circles, two-dimensional planes and spheres, and the four-dimensional space-time used in general relativity.
Differential manifolds are types of manifolds with a local differential structure, allowing for definitions of vector fields or tensors that create a global differential tangent space.
A Riemannian manifold is a differential manifold that comes with a metric tensor, providing a way to measure distances and angles.
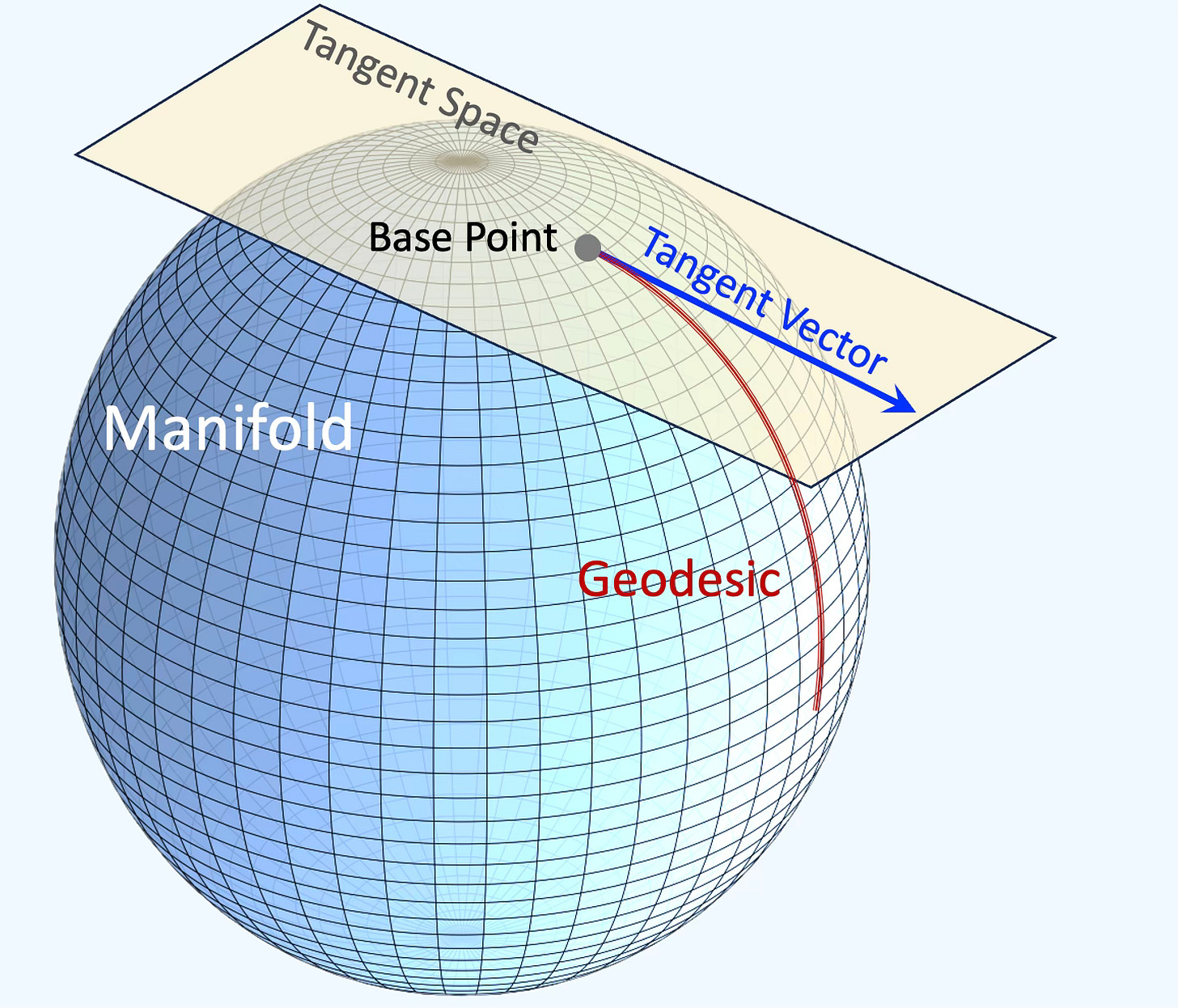
Fig 1 Illustration of a Riemannian manifold with a tangent space
SPD Matrices
Let's introduce our manifold defined as the group of symmetric positive definite (SPD) matrices. SPD matrices are used in a wide range of applications:
Diffusion tensor imaging (analysis of diffusion of molecules and proteins)
Brain connectivity
Dimension reduction through kernels
Robotics and dynamic systems
Multivariate principal component analysis
Spectral analysis and signal reconstruction
Partial differential equations numerical methods
Financial risk management.
A square matrix A is symmetric if it is identical to its transpose, meaning that if aij are the entries of A, then aij = aji. This implies that A can be fully described by its upper triangular elements.
A square matrix A is positive definite if, for every non-zero vector b
If a matrix A is both symmetric and positive definite, it is referred to as a Symmetric Positive Definite (SPD) matrix. This type of matrix is extremely useful and appears in various real-world applications. A prominent example in statistics is the covariance matrix, where each entry represents the covariance between two variables (with diagonal entries indicating the variances of individual variables). Covariance matrices are always positive semi-definite, and they are positive definite if the covariance matrix has full rank, which occurs when each row is linearly independent from the others.
The collection of all SPD matrices of size n×n forms a Riemannian manifold. It is also a Lie group with a natural geometric structure.
The Mahalanobis distance is a metric deeply connected to Symmetric Positive Definite (SPD) matrices, particularly through the covariance matrix, which is a key example of an SPD matrix.
Exponential and Logarithmic Maps
The exponential & logarithmic maps and parallel transportation are crucial for Riemannian approaches in machine learning. On any manifold, distance are defined as geodesics that correspond to straight lines in Euclidean space as illustrated below:
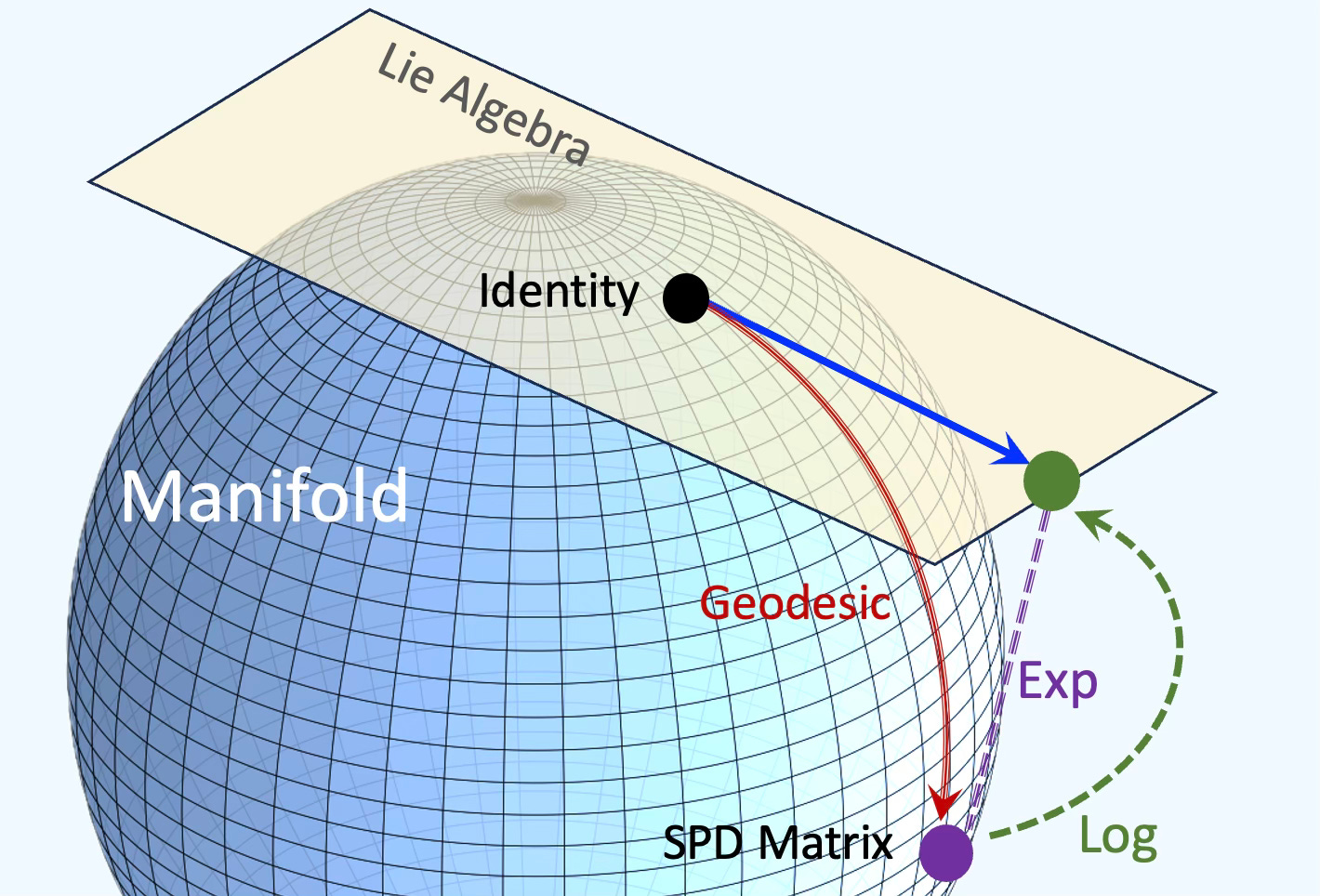
Fig. 2 Manifold with tangent space and exponential/logarithm maps
Let consider a vector x to y on a tangent space at point y. Operations on the point on the manifold rely on the exponential map (projection) onto the manifold. In the case of the binary logistic regression, the prediction on the manifold is defined by the exponential map expx.
Let select two Riemannian metrics for the SPD manifolds [ref 7]:
Affine invariant Riemannian metric
Log-euclidean Riemannian metric
Affine Invariant Riemannian Metric
For any two symmetric positive definite (SPD) matrices A and B, the Affine Invariant Riemannian Metric (AIRM) between them is defined as:
Log-Euclidean Riemannian Metric
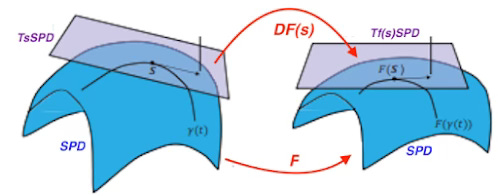
Given a symmetric positive definite matrix SPD at point S and a tangent space T(s)SPD, the logarithmic and exponential maps can be expressed as:
. . Fig. 3 Illustration of the log-euclidean metric for SPD
⚙️ Hands-on with Python
Environment
Libraries: Python 3.11, SciKit-learn 1.4.2, Matplotlib 3.9.1, Geomstats 2.7.0
Source code: Github.com/patnicolas/geometriclearning/geometry/manifold
Note: To enhance the readability of the algorithm implementations, we have omitted non-essential code elements like error checking, comments, exceptions, validation of class and method arguments, scoping qualifiers, and import statements.
Geomstats is an open-source, object-oriented library following Scikit-Learn’s API conventions to gain hands-on experience with Geometric Learning. It is described in article Introduction to Geomstats for Geometric Learning
Implementation
🔎 Designing components
First, let's create a data class, SPDTestData that encapsulates the training features X and label y. This class will be used to validate our implementation of logistic regression on SPD manifolds using various metrics, as well as in Euclidean space.
The flatten method in code snippet 1 vectorizes each 2-dimension SPD matrix entry in the training set to be processed by the scikit-learn cross validation function.
We wrap the generation of random data, SPD manifolds and the evaluation of various metrics in the class BinaryLRManifold (code snippet 2).
The generation of the labeled training set uses the numpy random values generation method.
🔎 Generating Data
The method __generate_spd_data create symmetric positive definite n_features x n_features matrices by computing eigenvalues of a random symmetric matrix. The symmetric matrix is computed using the transpose of the matrix as follows:
🔎 Creating Manifold
Creating an SPD matrix is straightforward:
Instantiate the Geomstats SPDMatrices class
Equip it with a Riemannian metric.
We creates two SPD manifolds with affine metric and log Euclidean Riemannian metrics (code snippet 5)
Evaluation
The initial phase involves verifying our implementation of the metrics related to SPD manifolds. This is achieved by calculating the cross-validation score for SPD matrices containing random values between [0, 1] and ensuring that the average score approximates 0.5.
🔎 Euclidean space
We utilize the logistic regression class and the cross_validate method from Scikit-learn once the contents of the matrix have been converted into a vector form.
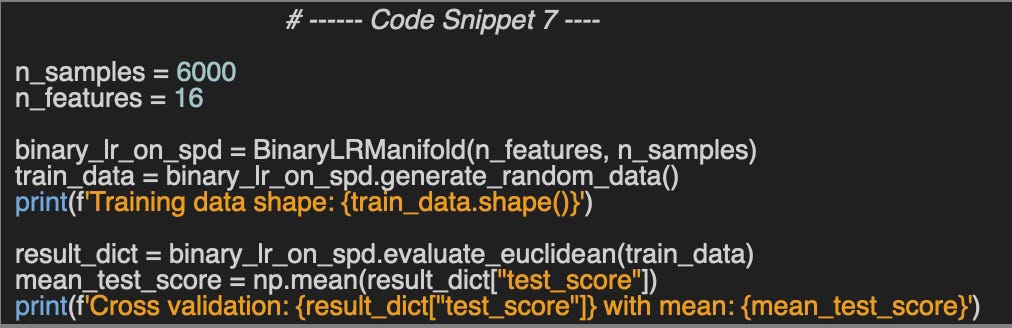
The test code used a training set of 6000 samples of 16 x 16 (256) SPD matrices. The binary logistic regression in the Euclidean space as a mean cross validation score of 0.487 instead of 0.5.
Cross validation: [0.478 0.513 0.497 0.474 0.471] with mean: 0.487🔎 Classification on SPD manifold
To utilize scikit-learn's cross-validation features, the SPD matrix must first be differentiated on its tangent space before applying logistic regression. These two steps are executed using a scikit-learn pipeline.
We employ the same training setup as used in the evaluation of logistic regression in Euclidean space, but we apply the log Euclidean (SPDLogEuclideanMetric) and affine invariant (SPDAffineInvariant) metrics. The mean values of the cross-validation scores are 0.492 and 0.5, respectively, which significantly improve upon the results from the Euclidean scenario.
Output for Log Euclidean metric:
Cross validation: [0.495 0.504 0.498 0.491 0.470] with mean: 0.492Output for affine invariant metric:
Cross validation: [0.514 0.490 0.490 0.490 0.504] with mean: 0.500🧠 Key Takeaways
✅ The Geomstats library significantly simplifies the implementation of traditional machine learning on manifolds.
✅ Logistic regression on manifolds outperforms its Scikit-learn counterpart for binary classification of symmetric positive definite matrices.
✅ The Log-Euclidean metric delivers better predictive performance compared to the affine-invariant metric.
📘 References
🛠️ Exercises
Q1: What two conditions must a Symmetric Positive Definite (SPD) matrix satisfy?
Q2: Which metric uses an SPD matrix as its covariance matrix?
Q3: In code snippet 9, what would be the mean test scores if a 32 × 32 SPD matrix (with n_features = 32) is used?
Q4: What is the formula for generating a random SPD matrix?
Q5: Which Python library is commonly used to implement binary logistic regression for SPD matrices?
👉 Answers
💬 News and Reviews
This section is focused on news and reviews of papers pertaining to geometric deep learning and its related disciplines.
Article review: Medical Application of Geometric Deep Learning for the Diagnosis of Glaucoma
This medical article assesses the effectiveness of geometric deep learning in diagnosing glaucoma using a single optical coherence tomography scan of the optic nerve. The study demonstrates that the 3D point cloud model, PointNet, outperforms convolutional neural networks in this task.
Patrick Nicolas has over 25 years of experience in software and data engineering, architecture design and end-to-end deployment and support with extensive knowledge in machine learning.
He has been director of data engineering at Aideo Technologies since 2017 and he is the author of "Scala for Machine Learning", Packt Publishing ISBN 978-1-78712-238-3 and Geometric Learning in Python Newsletter on LinkedIn.